5.2 Power, head and flow rate
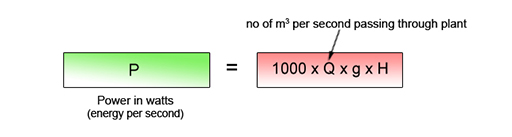
The power supplied by a plant, (the number of watts), is the rate at which it delivers energy: the number of joules per second. In a hydro plant this will obviously depend on the volume flow rate of the moving water - the number of cubic metres (m3) per second passing through the plant, usually represented by the symbol Q (think ‘Quantity’); g = acceleration due to gravity and H is ‘effective head’ of water.
It then follows from the equation shown in Figure 10 that this power will be:
However in any real system the water falling through a pipe will lose some energy due to frictional drag and turbulence, and the effective head will be less than the actual or gross head. These flow losses vary greatly - in some cases the effective head is no more than 75% of the actual height difference, in others as much as 95%.
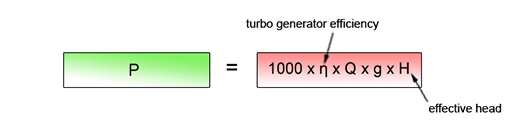
Then there are energy losses in the plant itself. Under optimum conditions, a hydroelectric turbo-generator is extremely efficient, converting all but a few percent of the input power into electrical output. Nevertheless, the efficiency (the ratio of the output power to the input power) is always less than 100%. With these factors incorporated, the output power becomes:
Box 2: accounting for losses
We’ve seen two ways in which different losses are accounted for: using the effective head, Heffective, rather than the gross head takes care of losses due to friction before the water reaches the turbine while the plant efficiency, η, accounts for the losses in the plant itself.
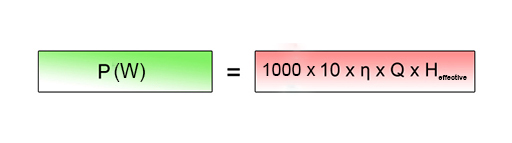
So, moving on, if we now use the approximations g = 10 m s–2 and ρ = 1000 kg m-3, we obtain a very useful simple expression:
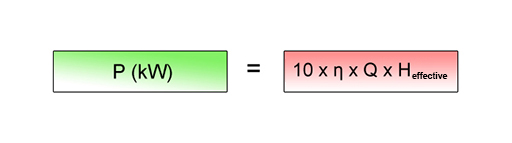
Activity 2 Calculating power output
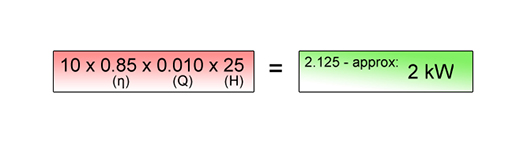
Use the equation shown in Figure 13 to work out the power output for a site which is a mountain stream with an effective head of 25 metres, turbo-generator efficiency of 0.85 and a modest flow rate of 600 litres a minute, which is 0.010 cubic metres per second.
Now you know how to work out how much power a plant can supply, you will now move on in the next section to look at the types of hydroelectric plant.