3.3 Multiplication and division

The next video demonstrates two methods for long multiplication and discusses the pros and cons of each method.

Download this video clip.Video player: Video 5 Two methods for long multiplication

Show transcript|Hide transcript

Transcript: Video 5 Two methods for long multiplication

INSTRUCTOR:

I am going to find the result of multiplying 74 by 36 first of all by using the grid method. This links to finding the area of a rectangle 74 units long and 36 units wide. I'm going to partition 74 and 36 into that tens and units, which will mean splitting the length of the rectangle into 70 and 4 and the width of the rectangle into 30 and 6. I'm now then to find the areas of the four parts of the rectangle. So the top left, 30 times 70, three 7's are 21.

So 30 times 70 is 2,100. Top right, 30 times 4 is 120. Bottom left six times 70 is 420. 6 times 4 is 24. So the area of the rectangle is the area of those four parts added up. I'll work out some of the numbers on the top row, that's 2,220. And the bottom row will be 444. And if I add those two up, I'll get the answer to 74 times 36 which is 2,664.

The beauty of the grid method is that the learner works out four products for a two digit by two digit calculation. And if any mistakes are made, it is easy to check where those mistakes are. The learner is also dealing with those numbers as the sum of their parts, 70 and 4, 30 and 6 in this case.

Another method of working out the same multiplication would be to use the standard column method. This is the traditional method, which has been taught for decades. So you would think that every adult would be proficient at it but surveys show that very few people in the general population are proficient at using the standard column method. So we'll look at that method now.

The numbers are written one underneath the other, 74, 36, and I put a multiplication at the side to remind us that that's what we're doing. We're going to have three lines of working. First of all, I'll multiply 74 by 6. Six 4's are 24. So I'll put down the 4 and carry the 2 very small in the next column. six 7's are 42 plus the two that I carried makes 44.

Then I come to multiply by the 3, remembering that it is actually 30. So to multiply by 30, I put down the 0 then carry on as if I were multiplying by 3. Three 4's are 12. So I put down the 2 and carry the 1 very small into the next column. Three 7's are 21 plus the one that I carried makes 22. And if I add those two lines up I got 2,664, the same as I did for the grid method. You might notice that they've got the same lines of working.

Now the standard column method is neat and quick if the learner knows how to do it correctly. However, for many learners, this method is fraught with difficulties. It treats each number as a string of digits, unlike the grid method which treats each number as the sum of its parts. This can mean the learner operates the standard column method according to the set of rules, and they can be easily forgotten or confused.

Some of the procedural problems I've seen are learners not knowing what to do with the carrying figures or forgetting to put down the 0 or not putting it in the units column but putting it at the side and getting lost during the working as they don't know their multiplication tables and need to work them out, whereas in the grid method, they still have to work out the multiplication table facts, but at least the other three boxes can wait for them. And there are no carrying figures to worry about.

End transcript: Video 5 Two methods for long multiplication

Download

Video 5 Two methods for long multiplication

Division is the arithmetic operation where learners experience the most difficulty. Division is the inverse of multiplication which means that it is possible to approach division by complementary multiplying. For example, to answer the question 78 ÷ 6 you can ask ‘How many 6s make 78?’.

One way to answer the question in this way is to use the ‘chunking’ method where you add ‘chunks’ of 6 until you reach 78. It saves having to add 6 at a time, which could be laborious. For example:

(you know that 78 is more than 6 lots of 10, so start there)

(you have 18 left to make the 60 up to 78, that’s 3 lots of 6)

So

Or you could start with 78 and keep subtracting 6 until you have nothing (or a number smaller than 6) left: For example:

Whether working up to 78 or down from 78, the method is basically finding how many 6s there are in 78. This method clearly becomes harder with larger numbers and requires knowledge of multiplication tables and good mental arithmetic. It is, however, an intuitive method of dividing.

The traditional method of division is known among teachers as either the bus stop method (because the working looks like a bus stop),or the ‘gazinta’ method (because you ask how many times 6 ‘goes into’ each number).

Figure 5 One formal method of short division

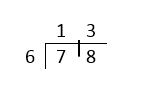
Figure 5 shows that 6 goes into 7 once with 1 left over. So, put the 1 (for the once) above the 7 and the 1 left over next to the 8. Now read it as 6 goes into 18, which is 3. Put the 3 over the 8. This is an easy method to operate if you can remember the procedure. It is not so easy to understand why it works. Yet many learners prefer it to having to use the ‘chunking’ method.

The bus stop method is efficient to use with larger numbers as well, as long as your multiplication tables are good, and you can do some mental calculation. When dividing by two-digit numbers, I prefer to use and to teach a version of this short division method.

Activity 9 Solving a division problem

Timing: Allow 10 minutes

Suppose you have 1960 pupils and teachers in a school to ferry to an event in buses which each carry 43 passengers. How many buses will be needed?

So, you are trying to find out how many times 43 goes into 1960 and you need an extra bus for the remainders.

Spend ten minutes ‘having a go’, using whichever method you prefer. Then watch the video.

Download this video clip.Video player: Video 6 Two ways to solve a division problem

Show transcript|Hide transcript

Transcript: Video 6 Two ways to solve a division problem

INSTRUCTOR:

How many buses do I need to carry 1,960 passengers if each bus carries 43? First, I will begin by using an intuitive method whereby I will add up multiples of 43 until I can carry all 1,960 people.

So I'm going to start by working out how many 10 buses would carry. 10 times 43 is 430. I obviously need a lot more than 10 buses. I will try 4 lots of 10 buses, which is 40 buses. That will be 4 times 430-- I could double and double again, that will give me 1,720 passengers. This is closer to 1,960, but adding another 10 buses will take me well over the 1,960, so I'm now going to add smaller numbers of buses.

I could add 5 buses. That'll be half of 430. So 5 times 43 will be 215. I'm going to add those together, just the last two lines, to give me 45 lots of 43. So that will be 1,935. So that's not quite enough passengers yet can be taken, so I need to add another bus. Let's try 46 buses by adding 43 onto my last figure. So that will give me 1,978. So I can definitely carry all 1,960 people, and they will also be 18 spaces left. So I need 46 buses.

The traditional way to work out how many buses are needed is to do a division. So I'm doing 1,960 divided by 43. I'm going to use a short division method even though I have a two-figure number as a divisor. Years of teaching experience shows me that learners struggle with the long division method with its complicated procedure.

So 43 into 1,960, I'm going to have to work out how many 43's are in 196. So I'm going to write the 43 times table down the side. So two of them will be 86, three will be 129, four will be 172. So that's below 196, but another 43 would take it over. So 43 is into 196. It must be 4, then of course, it's actually 443-- this is 172, so there's a remainder of 24, which I put next to the 0, and read it as 240.

So 43 is into 240, I just need to go a bit further with my 43 times table, add another one of those on. So that's 215. That's just less than 240. Another 43 would take it over, so 43 is into 240, go 5. And of course, five 43's a 215. So there's a remainder of 25.

So we've got an answer-- 45 remainder 25. What does remainder 25 mean? Do 25 people have to walk? We can't have that, so I will order them another bus. So altogether, I will need 46 buses.

End transcript: Video 6 Two ways to solve a division problem

Download

Video 6 Two ways to solve a division problem

Interactive feature not available in single page view (see it in standard view).