1.4 Using concrete resources
It is important to give learners of all ages a variety of concrete experiences connected with proportional reasoning to encourage them to compare, make conjectures, find relationships and generalise their learning.
Young learners may start with weighing and measuring objects in the classroom, and discussing comparisons between amounts.
Activity 6 Sharing money
When asked to share out £24 between two cousins in the ratio of 3:1, learners can use counters to represent the pounds (Figure 7). How can you use counters to demonstrate the solution to this problem? Write responses in the box below.
Discussion
Grouping counters in groups of 1 and 3 is one way to work on this problem.
By grouping counters in this way, learners share out all the counters in the ratio of 1:3.
They can then look at how many of each colour there are altogether. Noticing that there are 6 groups of 3 and 6 groups of 1 would result in finding a total of 18 blue counters and 6 yellow counters, representing the £18 and £6 the cousins will each get.
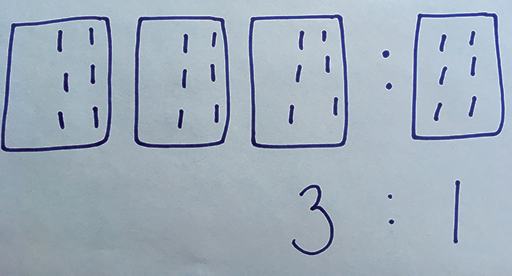
Another way to approach this problem using counters is to create boxes (on paper or on mini-whiteboards) to represent the ratio. In this case, since the ratio is 3:1, you will need 3 boxes for the first cousin and 1 box for the second cousin.
The counters, which represent pounds, are then shared out equally between the 4 boxes. The first cousin is given 3 boxes, so receiving £18, and the second cousin is given 1 box, so receiving £6 (Figure 8).
This approach can also be used with pens on mini-whiteboards. Learners need to create the boxes to represent the ratio and then put a mark in every box until they get to the total, in this case 24 (Figure 9).
This imagery can then support learners in moving towards a more abstract concept of sharing amounts into a ratio. In other words, it can help them to understand that in a ratio of 3:1 there are 4 equal parts in total which the £24 needs to be divided equally between.
Note: When moving on to ratio problems involving fractions and decimals, using manipulative resources can become problematic. It is sensible to move onto more abstract methods with your learners before introducing these kinds of problems.