2.1 Representations
The work of Jerome Bruner (1966) has been influential in early algebra. He identified three modes of representation for mathematical objects: the enactive, the iconic and the symbolic, which move broadly from the concrete to the abstract. Learning a new concept is supported by meeting each of these modes and translating between them.
- In the enactive mode, the concept is represented through learners acting on concrete, physical objects. For algebra, the concept of an unknown quantity can be represented by a bag or tin containing an unknown number of counters. The teacher can ask questions such as 'What happens if three counters are placed in a tin? What if one counter is taken out? What if there are ten tins with the same number of counters in each?' A variable can be represented as a changing length, for example learners can measure the height of a sunflower.
- In the iconic mode, a picture illustrates the unknown quantity (Figure 3). The picture takes its meaning from the learner’s previous enactive experiences.
- In the symbolic mode, the concept is represented in an abstract or a conventional way. Bruner considers words (such as ‘five’, ‘add’ or ‘tin’) to be symbolic in the same way as conventional letters and signs are (e.g. 5, + or t).
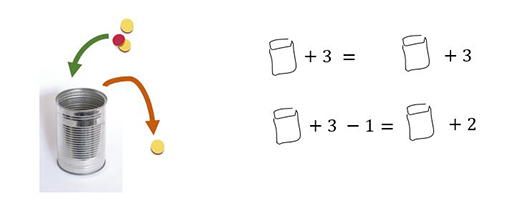
Concrete–pictorial–abstract
Some teaching traditions describe a learning progression through concrete–pictorial–abstract and develop their materials accordingly. There are often intermediate stages in the final translation towards symbols/abstract representations. For example, Figure 3 shows two different pictorial/iconic representations of the tin activity. One use photographs of objects and arrows that represent the actions of adding and taking away counters. In the other, the learner has drawn their picture of a tin and combined it with familiar symbols such as +, 3 and =.
Bruner’s three modes offer a useful way of planning for progression, but their order does not have to be interpreted too strictly. Teachers have found that even young children can reason algebraically about a quantity that they have not handled, when the meaning is carefully established through discussion. Equally, what feels concrete or abstract to a learner can change with experience. Words such as the ‘price of a book’ are considered as symbolic for younger learners, but they can feel iconic once their language has developed. For example, learners often choose to use symbols such as b (book) or p (price) which remind them of the words they are using for a quantity. A learner studying A-level mathematics will be able to use x, y or any other letter for the price and will eventually have enough experience of manipulating symbols with pencil and paper that this will start to feel like a concrete activity on which she can base further learning.
Making sense of symbols
Research in early algebra suggests that learners need to establish meaning in two ways. First, they need to understand how calculations and arithmetical relationships between quantities are expressed using the familiar symbols for numbers and operations. This is why teachers emphasise forming mathematical sentences in words and in number symbols as well as calculating answers. Second, learners need to make sense of working with an algebraic symbol to represent an indeterminate quantity. These are both necessary stages, which lay the foundations for manipulating symbols out of a context. If learners move too quickly to symbolic representation they risk interpreting the symbols incorrectly, introducing misconceptions that use their prior experiences from number work to deal with the troublesome letter.
Activity 6 Reflecting
Look at this question and the range of responses. Which would you expect to see from your learners (try it with them)? What is the misconception that underlies each answer?
When you have finished the task watch the video.

