3.1 Relational understandings
Treating the equals sign as a relation is important for two aspects of algebraic thinking. The first is maintaining equal value. The two expressions on either side of the equals sign are equivalent; their values balance. Anything that is done to one side of the equation must be done to the other side, in order to keep that balance. This aspect is seen in the common metaphor of an equation as a balance scale (Figure 8).
Sometimes this aspect is referred to as sameness. However, looking at the balance makes it obvious that there is not the same expression on both sides. Instead, they have equal value.
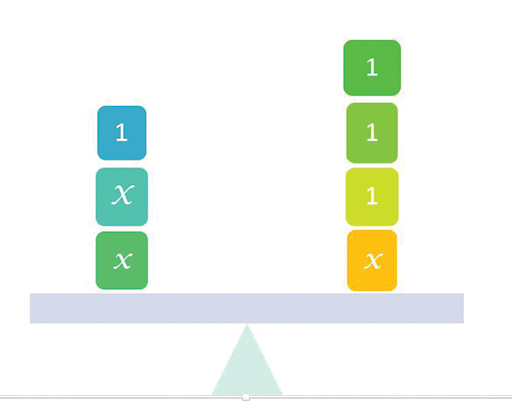
What is the equation represented by this balance?
What happens if you take 1 from both sides of this balance? If you take the number represented by x from both sides?
The second benefit of the relational understanding of the equals sign is that it allows substitution. If two expressions are equal in value then one can be substituted for the other. This is useful in simplifying expressions and solving equations.
You met substitution in the symbol grid activities. Watch the video below to see how.
The equals sign as substitution is used twice in this process: the first time it is used to replace an indeterminate quantity (expressed symbolically as a sum) with a number that has equal value. The second time the recall of number facts is used to determine a number that could be substituted for symbolic quantities, and a new equation can be written.

Substitution or ‘do the same to both sides’
It is useful for teachers to be aware of the substitution aspect of the equals sign as learners will use this in their speech. They are likely to draw on the substitution when they know the number facts involved (here it is 9 + 6 that equals 15). When they do not know the number facts, they will use the principle of ‘maintaining equal value’ and ‘do the same to both sides’ in order to work out 15 – 9 = 6. Both aspects need to be recognised and taught.
