Moving on to description
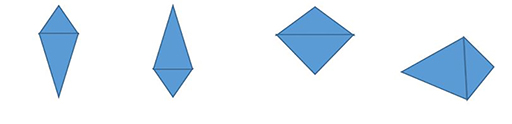
Learners develop an intuitive feel for the look of a shape: the squareness of a square, the circular nature of a circle, and so on. If learners only see and experience ‘typical’ examples of each kind of shape then they may not accept shapes which are in unusual proportions or orientations. For example, the shapes in Figure 3 are all kites but only the first one is typical of the orientation and proportion shown in textbooks and on classroom posters.
You can be sure that these shapes are indeed kites if the properties of a kite hold true for these shapes.
Activity 1 Properties of a kite
Write down as many properties of a kite as you can think of. Remember to use angle sizes, side lengths and symmetry.
Discussion
Here are some properties of the kite:
- Four sides, i.e. the kite is a quadrilateral.
- Two pairs of adjacent equal length sides (adjacent means the sides are next to each other).
- One pair of opposite equal angles.
- One line of symmetry.
- No rotational symmetry or rotational symmetry of order 1 (i.e. there is only one position where you can fit the kite in a 360⁰ turn).
Once learners are able to describe shapes by listing their properties they will accept unusually orientated or proportioned shapes such as the kites in Figure 3. They can progress to solving simple geometrical problems using the properties of the shapes that they know.
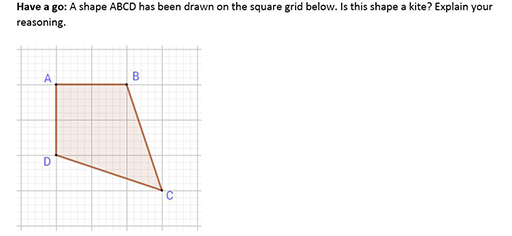
Activity 2 Is this a kite?
Discussion
ABCD is a kite.
Adjacent sides AB and AD are equal in length (2 units).
Adjacent sides BC and BD are equal in length (they are both the diagonals on 3 by 1 rectangles).
AC is the line of symmetry. (Points A and C are on the line. Points B and D are both one diagonal of a square away from line AC.)
Activity 3 Beginning to reason abstractly
In Activity 1 you listed the properties of a kite. Now work out a definition of the kite which uses only two or three of its properties. These properties are known as the necessary and sufficient conditions. There is more than one way to write a definition of the kite.
Discussion
Here are some definitions of the kite using necessary and sufficient conditions.
- A quadrilateral with two pairs of adjacent equal sides.
- A quadrilateral with a line of symmetry and a pair of opposite equal angles.
Did you think of any others?