2.2 Quadrilaterals
In this section you will explore how certain quadrilaterals can be made from triangles.
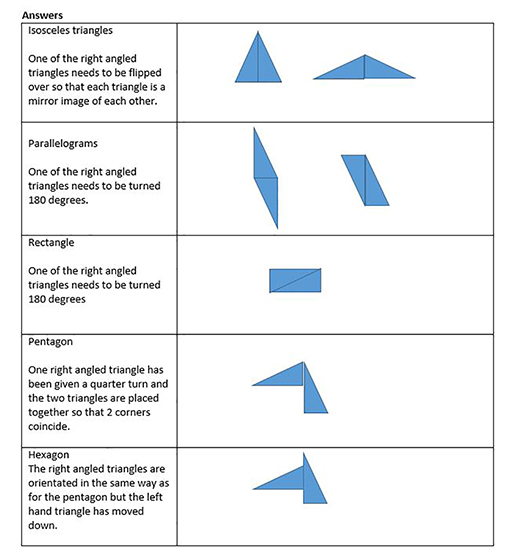
Activity 7 Making shapes out of two congruent right-angled triangles
Draw and cut out two congruent right-angled triangles. (Congruent means they are exactly the same size and shape, same angles, etc.)
Can you make the following shapes by placing the congruent right-angled triangles together along two of their edges (i.e. no overlapping)?
- 2 different isosceles triangles
- 2 different parallelograms
- 1 rectangle
- 1 pentagon
- 1 hexagon
Activity 8 Reflecting a triangle in one of its sides
Draw a triangle (not a special triangle) and then draw a reflection of that triangle in one of its sides. Keep both the original triangle and the reflected triangle which should now make a quadrilateral. What kind of quadrilateral do you get?
Then do the next activity and read the discussion afterwards.
Activity 9 Reflected triangle in Geogebra
Click on this link https://www.geogebra.org/ m/ U6azsQb6 [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] which takes you to a Geogebra file that contains one triangle which has been reflected in one of its sides. ‘Drag’ the resulting quadrilateral to investigate which shapes you can make. (If you have difficulty in opening the link, go to www.geogebra.org and search for ‘triangle reflected in one of its sides’.)
Discussion
You can drag the figure at the link above if you have clicked on the arrow tool (which is the default tool when you open a Geogebra file) and then you drag the figure on the screen. Were you able to make any of the following?
- a kite
- a rhombus
- a square
- a isosceles
- an triangle
Activity 10 Splitting quadrilaterals
Which quadrilaterals can be split into two congruent triangles? Complete the table in Figure 8. The third column refers to whether the triangles are reflected or rotated in the quadrilateral.
Discussion
The table can be completed as shown in Figure 9.
These tasks are a novel way to approach learning about triangles and quadrilaterals. They encourage learners to think about the shapes and their properties. Many textbook exercises consist of questions asking learners to recall shape properties, without requiring learners to think deeply about them.
The special quadrilaterals – those we have names for – are special because they have interesting properties such as symmetry, which relates to the triangles which make them up.