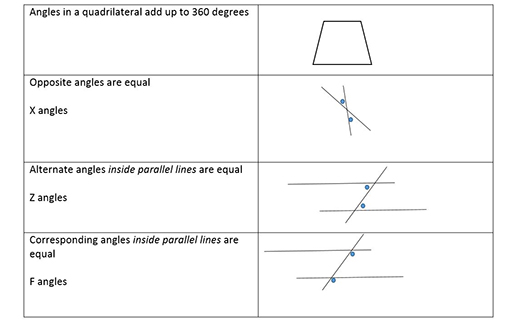
3.2 Angle sum of triangles
The angles of any triangle sum to 180⁰. This can be proved in several ways and can easily be shown to convince learners as a classroom activity.
Activity 5 Demonstrating the angle sum of a triangle
You will need paper, pen, ruler and scissors.
Draw any triangle and mark the angles at the corners.
Cut out the triangle.
Tear off the corners then put the corner angles together. They should all form a straight line.
If we accept that there are 360⁰ in a circle and 180⁰ on a straight line then we have shown that the three corners add up to 180⁰.
Discussion
This activity can be done in the classroom. If 30 learners can do this activity using 30 different triangles then they will have demonstrated the angle sum of a triangle in 30 different ways. This is not a proof, merely a demonstration that it works.
It is much more fun for learners if they discover angle facts for themselves, rather than being simply told them.
Think of other ways for learners to discover the angle facts using drawing and cutting, and measuring using a protractor.
Activity 6 A problem using angle facts
Below is a design using 8 congruent (i.e. exactly the same size and shape) rhombuses. Calculate the two different angles in the rhombuses.
Discussion
Think about the number of rhombuses which meet in the middle of the design. Their sum must be 360⁰.
Think about the rhombus as a quadrilateral. Its angles must sum to 360⁰. A rhombus has two pairs of equal angles.
Use compasses and a protractor to recreate this design. Begin by drawing a circle and marking off 8 equally spaced points on the circumference. Use these points to draw the bottom halves of the 8 rhombuses.
To find the top points for each rhombus use the compasses opened to the same radius as when you drew the circle. Draw 2 arcs (parts of circles) from each point which will intersect in pairs above the rhombus halves. These intersections are the top points of the rhombuses. Join these to the circumference to complete the rhombuses.