2.2 Analysing data using measures of central tendency and spread

The mean, median and mode are measures of central tendency. Each of these averages gives an indication of the typical or central value in the data set.

The range is a measure of spread. It tells us how much a data sample is spread out or scattered.

These measures can be used to summarise a data set and help us to make conclusions about what the data shows.

The mean

The mean is the most common measure of average. To calculate the mean, add the numbers together and divide the total by the amount of numbers:

Mean = sum of numbers ÷ amount of numbers

Activity 8 Sharing sweets fairly

Timing: Allow 5 minutes

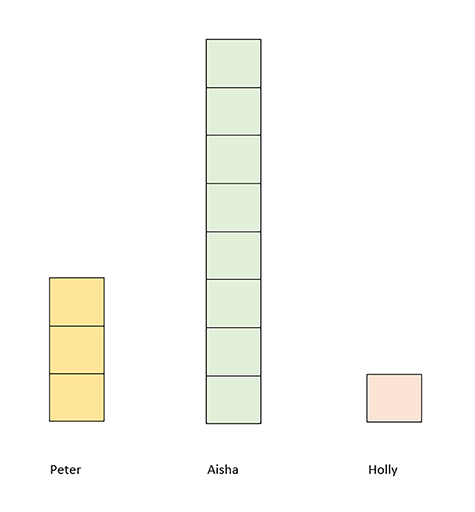
Three friends have each been given some sweets (Figure 10).

Peter has 3 sweets, Aisha has 8 sweets and Holly has 1 sweet.

How could the sweets be shared fairly between the three friends?

Figure 10 Sharing sweets with friends

Show description|Hide description

A photo showing three children in Halloween outfits holding sweets.

Figure 10 Sharing sweets with friends

Discussion

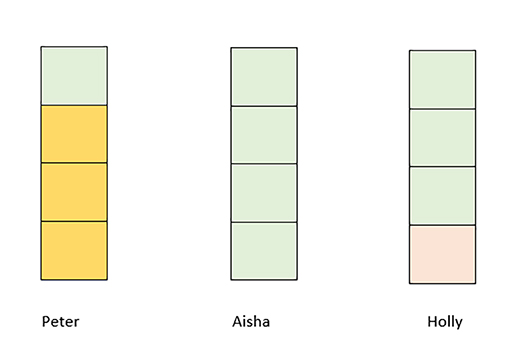
This question is asking for the mean average. Between the 3 children there are 12 sweets. Dividing this by 3 would mean that each friend receives 4 sweets.

The mean average is 4.

Activity 9 Reflecting

Timing: Allow 5 minutes

How would you present the question above to your learners?

How would you help them to understand what the mean represents?

Discussion

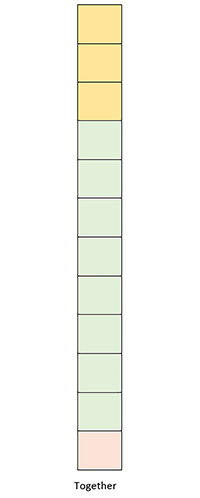
Using concrete resources such as counters, cubes or coins can help learners to understand the concept of the mean average (Figure 11). They can physically move the objects to share them out evenly.

Figure 11 Finding the mean with concrete resources

Show description|Hide description

Some photographs showing how Cuisenaire rods can be used to calculate the mean. Cuisenaire rods of length 10, 6 and 8 are shown in the first image. Then these are replaced to show three bars of length 6, with four white unit rods added to make 10, and two unit rods to make 8, so that the three totals are still 10, 6 and 8. In the third image the white unit rods are shown to be moving. In the fourth and final image, the white unit rods have been share equally so that the three rods of length 6 each have two white unit rods, giving three totals of 8. The words “Mean =8” are written next to this final image.

Figure 11 Finding the mean with concrete resources

This can become more challenging when learners are required to find fractions of amounts.

For example:

If four learners have 3, 5, 4 and 2 cubes respectively, what is the mean number of cubes?

3 + 5 + 4 + 2 = 14

14 ÷ 4 = 3½

IIn this example, cubes could be used to show that each learner gets 3 cubes and that there are 2 cubes left over. Depending on the age and experience of the learners, they can then record the mean as 3 remainder 2, or they can discuss how to share the remaining two cubes between four.

It can be helpful to have objects which can be split in half, when working on problems like this for the first time, including edible resources!

Another way would be to use pictorial representations of the problem (see Figures 12 to 14).

Figure 12 A diagram which represents the number of sweets each child has

Show description|Hide description

A pictorial representation of the number of sweets three children (Peter, Aisha and Holly) have. There is a rectangle above Peter’s name made up of 3 yellow squares, the rectangle about Aisha’s name is made of 8 blue squares and there is 1 pink square above Holly’s name.

Figure 12 A diagram which represents the number of sweets each child has

Figure 13 All sweets together

Show description|Hide description

The three rectangles in figure 12 have been combined to make one long rectangle of length 12. It is made up of 3 yellow square, 8 blue squares and 1 pink square.

Figure 13 All sweets together

Figure 14 All sweets shared equally between three children

Show description|Hide description

This is a pictorial representation of the mean of the sweets. There are three equally sized rectangles each made of 4 squares above each of the names: Peter, Aisha and Holly.

Figure 14 All sweets shared equally between three children

With pictorial representations, halves, quarters and other fractions can be represented more easily.

The mode

The mode is the value that occurs most often.

The mode is the only average that can have more than one value.

When finding the mode, it helps to order the numbers first.

For example, here are the ages of a group of learners:

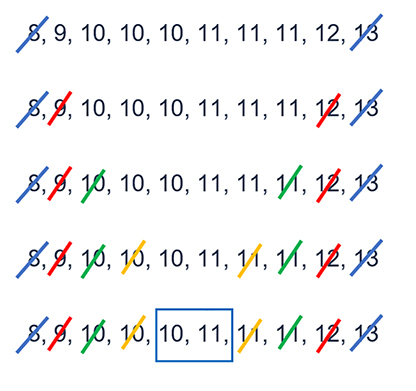
10, 8, 11, 9, 10, 12, 13, 11, 10, 11

Putting them in order, from smallest to largest, we have:

8, 9, 10, 10, 10, 11, 11, 11, 12, 13

There are three 10s and three 11s, so there are two modes.

We can call this data set bi-modal. The mode is 10 and 11.

The median

The median is the middle number in an ordered set.

If there are two middle numbers, the median is the mean of those two numbers.

For example, using the same ordered set of data as above, the two middle numbers are 10 and 11, so the median is 10.5 (Figure 15)

Figure 15 Calculating the median

Show description|Hide description

A diagram showing how the median is calculated. There is an ordered set of value which has been written out six times. Each list shows one more pair of “outside” values (the largest and the smallest) being crossed off. This is repeated until there are only two central values remaining: 10 and 11.

Figure 15 Calculating the median

The median is the mean of the two middle values 10 and 11. So the median is 10.5.