3 Fractions
What is a fraction?
A fraction is defined as a part of a whole. So for example , or ‘one third’, is one part of three parts, all of equal size.
Fractions are an important feature of everyday life. They could ensure that you get the best deal when shopping – or that you receive the largest slice of pizza! As you go through this section, you’ll see how fractions could be used when you are shopping or within the workplace.
Fractions are related to decimals and percentages, which you’ll look at in the sections that follow this one.
This section will help you to:
- order and compare fractions
- identify equivalencies between fractions
- calculate parts of whole quantities and measurements (e.g. calculate discounts in sales).
Please look at the following example before you carry out the activity:
A half can be written as , i.e. one of two equal parts.
A quarter can be written as , i.e. one of four equal parts.
An eighth can be written as , i.e. one of eight equal parts.
Box _unit2.3.1
Hint: The top of the fraction is called the numerator. The bottom of the fraction is called the denominator. Notice that is bigger than , even though the denominator 2 is smaller than the denominator 4. How would you explain one third? How would you write it as a fraction? Which is bigger: one third or two quarters?
Case study _unit2.3.1 Example: Where there’s a will, there’s a fraction
Lord Walton draws up a will to decide who will inherit the family estate. He proposes to leave of the estate to his son, to his daughter and to his brother.
- Who gets the biggest share?
- Who gets the smallest share?
Method
When numerators of fractions are all 1, the larger the denominator of the fraction, the smaller the fraction.
Looking at the example above, the fractions can be put in order of size starting from the smallest:
Extract _unit2.3.1
, ,
So:
- The biggest share () goes to his son.
- The smallest share () goes to his brother.
If you’re asked to arrange a group of fractions into size order, it’s sometimes helpful to change the denominators to the same number. This can be done by looking for the lowest common multiple – that is, the number that all of the denominators are multiples of.
Case study _unit2.3.2 Example: Looking at equivalent fractions
Arrange the following fractions in order of size, starting with the smallest:
- , ,
Method
The lowest common multiple is 12:
- 6 × 2 = 12
- 3 × 4 = 12
- 12 × 1 = 12
Whatever you do to the bottom of the fraction you must also do to the top of the fraction, so that it holds the equivalent value. The third fraction, , already has 12 as its denominator, so we don’t need to make any further calculations for this fraction. But what about and ?
- 2 × means calculating (2 × 3 = 6) and (2 × 6 = 12), so the equivalent fraction is
- 4 × means calculating (4 × 1 = 4) and (4 × 3 = 12), so the equivalent fraction is
Now you can now see the size order of the fractions clearly:
- , ,
So the answer is:
- , ,
Use the examples above to help you with the following activity. Remember to check your answers once you have completed the questions.
Activity _unit2.3.1 Activity 8: Fractions in order of size
- Put these fractions in order of size, with the smallest first:
- , , , ,
Answer
Remember that when the numerator of a fraction is 1, the larger the denominator, the smaller the fraction.
From smallest to largest, the order is:
- , , , ,
- What should you replace the question marks with to make these fractions equivalent?
- =
- =
- =
- =
Answer
- =
- =
- =
- =
Case study _unit2.3.3 Example: Drawing the fractions
If you need to compare one fraction with another, it can be useful to draw the fractional parts.
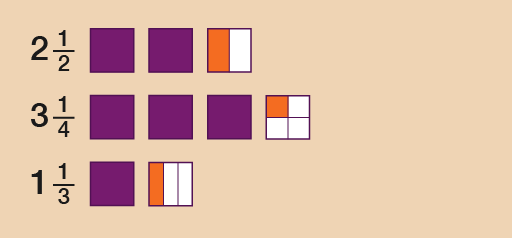
Look at the mixed numbers below. (A mixed number combines a whole number and a fraction.) Say you wanted to put these amounts in order of size, with the smallest first:
Extract _unit2.3.2
2 , 3 , 1
Method
To answer this you could look at the whole numbers first and then the fractional parts. If you were to draw these, they could look like this:
So the correct order would be:
Extract _unit2.3.3
1 , 2 , 3
Use the example above to help you with the following activity. Remember to check your answers once you have completed the questions.
Activity _unit2.3.2 Activity 9: Putting fractions in order
- Put these fractions in order of size, smallest first:
- 5 , 6 , 2
- Put these fractions in order of size, smallest first:
- 2 , 1 , 2
Answer
- The correct order would be:
- 2 , 5 , 6
- In this case, even though is bigger than and is bigger than , you need to look at the whole numbers first and then the fractions. The diagram illustrates this more clearly:
- The correct order would be:
- 1 , 2 , 2