3 Scale drawings
Have you ever drawn a plan of a room in your house to help you work out how to rearrange the furniture? Or maybe you’ve sketched a plan of your garden to help you decide how big a new patio should be?
These pictures are called scale drawings. The important thing with scale drawings is that everything must be drawn to scale, meaning that everything must be in proportion – that is, ‘shrunk’ by the same amount.
All scale drawings must have a scale to tell us how much the drawing has been shrunk by.
Case study _unit5.3.1 Example: In the garden
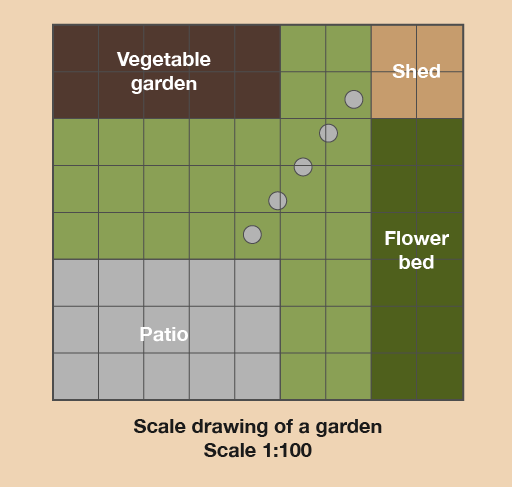
Here is an example of typical scale drawing:
What’s the width and length of the patio?
Box _unit5.3.1
Hint: This scale drawing has been drawn on squared paper. This makes it easier to draw and understand. Each square is 1 cm wide and 1 cm long. So instead of using a ruler you can just count the squares and this will tell you the measurement in centimetres.
Method
The scale in this drawing is 1:100. This means that 1 cm on the scale drawing is equal to 100 cm, or 1 m, in real life. Once we know the scale, we can measure the distances on the drawing.
Using a ruler (or just counting the squares), we find that the patio is 5 cm long and 3 cm wide on the drawing. This means that in real life it is 5 metres long and 3 metres wide.
So when you’re working with scale drawings:
- Find out what the scale on the drawing is.
- Measure the distance on the drawing using a ruler (or count the number of squares, if that’s an option).
- Multiply the distance you measure by the scale to give the distance in real life.
Now try the following activity. Remember to check your answers once you have completed the questions.
Activity _unit5.3.1 Activity 6: Getting information from a scale drawing
- Let’s stay with this scale drawing of the garden.
- a.What is the width and length of the vegetable garden?
- b.What is the width and length of the flower bed?
- c.How far is the patio from the vegetable garden?
- d.Say you wanted to put a trampoline between the patio and the vegetable garden. It measures 3 m by 3 m. Is there enough space for it?
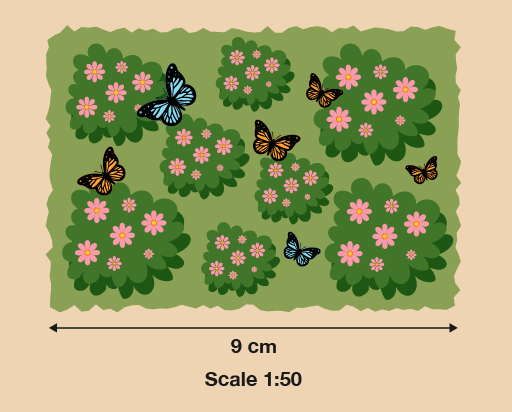
- A landscaper wants to put a wild area in your garden. She makes a scale plan of the wild area:
What is the length of the longest side of the actual wild area in metres?
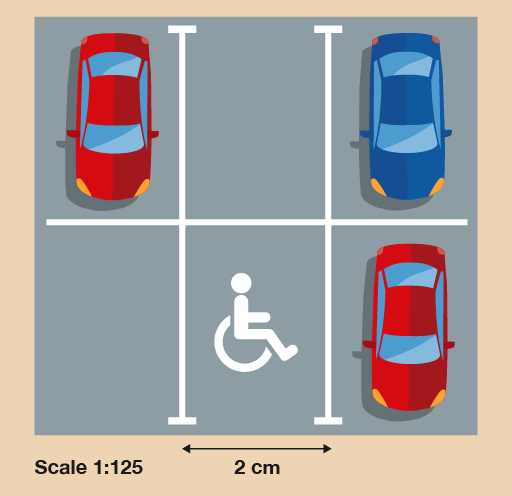
- Here is a scale drawing showing one disabled parking space in a supermarket car park. The supermarket plans to add two more disabled parking spaces next to the existing one, with no spaces between them.
What will be the total actual width of the three disabled parking spaces in metres?
Answer
- The answers are as follows:
- a.The vegetable garden is 5 m long and 2 m wide.
- b.The flower bed is 6 m long and 2 m wide.
- c.The patio and vegetable garden are 3 m apart.
- d.The distance between the patio and vegetable garden is 3 m and the trampoline is 3 m wide. So the trampoline would fit in the space, but it would be a bit of a squeeze.
The length on the drawing is 9 cm, and the scale is 1:50. This means that 1 cm on the drawing is equal to 50 cm in real life. So to find out what 9 cm is in real life, you need to multiply it by 50:
- 9 × 50 = 450 cm
The question asks for the length in metres, so you need to convert centimetres into metres:
- 450 ÷ 100 = 4.5 m
The actual length of the wild area will be 4.5 m.
You need to find out the width of three disabled parking spaces. The width of one parking space on the scale drawing is 2 cm, so first you need to multiply this by 3:
- 2 × 3 = 6 cm
The scale is 1:125. This means that 1 cm on the drawing is equal to 125 cm in real life. So to find out what 6 cm is in real life, you need to multiply it by 125:
- 6 × 125 = 750 cm
The question asks for the length in metres, so you need to convert centimetres into metres:
- 750 ÷ 100 = 7.5 m
The actual width of all three parking bays will be 7.5 m.
Summary
In this section you have learned how to use scale drawings.