2.3 Comparing algebraic expressions
Learners find it easier to follow word problems that are posed in a way that matches a typical sentence structure, such as the THOAN problems above. However, even a small variation on these will start to disrupt the order. For example, it is much harder to work on a problem like this one (which comes from an examination for 11-year-olds):
Younus takes three large letters to the Post Office. He pays with a £20 note. He gets change of £14.80. How much did each letter cost to post?
Earlier you have seen there is a progression in moving from working with a quantity that represents a specific unknown to one that can take a range of values. You will return to the ideas of variables and generality from a different perspective in Week 5, when you will look at introducing functions.
In the middle years, learners will move between these perceptions of number as they tackle different problems. Some learners strongly prefer to think of an unknown quantity as having a specific value. They experience what researchers call ‘a compulsion to calculate’. You can test this preference by asking diagnostic question such as these:
Activity _unit5.2.4 Activity 9 Reflecting
How did you answer these questions?
Did you choose specific values for m and n? Do you see now that you did not need to?
Discussion
The answers are: 11, 51 and 17.
The first question involves such a familiar number bond that you are very likely to have thought of: m as 6.
The second was chosen to have the same structure but vary the number involved so that it becomes easier for you to pay attention to the comparison of 2m and 2m – 1. Some of your learners will not do this. Instead they will work out m = 26 and then calculate .
The third question again has a similar structure but here m and n can take a range of values, so they are not specific unknowns. Again, some learners will choose values, for example 10 and 5, and then work out 10 + 5 + 2 = 17. Some will show awareness that these are not the only possible values by trying another pair, for example 7 and 8.
Another way is to use tasks that allow learners to treat quantities as variables while providing some support by being embedded in a number context.
The strategies discussed above lead learners to a correct answer but they reveal the ‘compulsion to calculate’. These learners have difficulty in dealing with unknowns by comparing algebraic expressions, and this will prevent their progression to more complex algebra.
One way of working on this difficulty is for teachers to ‘productively linger’ with algebraic problems – asking learners to explain their thinking and listen to others. Obtaining the answer is not enough: learners should use two different methods and be able to compare them.
Activity _unit5.2.5 Activity 10 Symbol sums
This task involves working with several unknowns and there are several different ways to approach it. Have a go at it yourself.
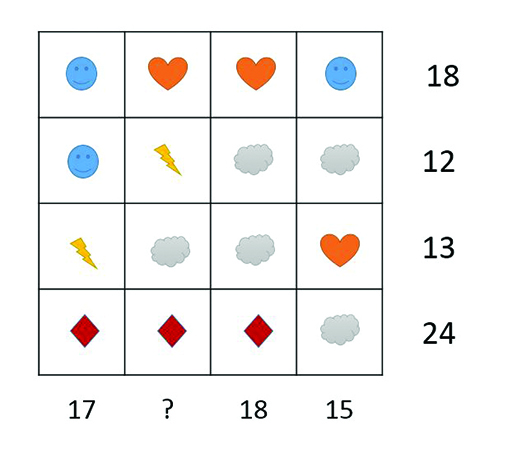
Each symbol in the grid in Figure 5 has a value. The totals of the rows and columns are shown. Can you find what each symbol is worth?
Activity _unit5.2.6 Activity 11 Thinking points
- Where would you encourage learners to start?
- How long would you leave learners to work independently before you ask them to listen to other people’s strategies?
- What kind of verbal explanations would you expect from learners? How do you want them to record their thinking?
- Is the task finished when the first learner works out the values? How could you ‘productively linger’ over this task to encourage algebraic thinking?
You can find a similar activity at https://nrich.maths.org/ 1053 [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)]
Discussion
You could start the problem in several ways:
The first row gives you the sum of heart and smiley.
Compare it with the fourth column to find the value of a cloud.
Compare the second and third rows to find that heart is 1 more than smiley.
The fourth row shows a cloud has to be a multiple of 3: try 3 or 6 or 9.
Compare the third and fourth column to see that a diamond is 3 more than a smiley.
The third row and third column show a diamond is 5 more than a lightning.
Activity _unit5.2.7 Activity 12 Symbol sums continued
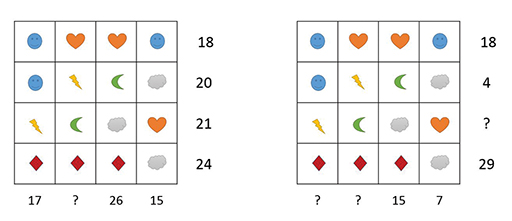
It is a good exercise of your own mathematical knowledge to invent similar problems and check that they can be solved.
In the two grids in Figure 6, the symbols in the grid are the same but the level of mathematics is slightly harder. Can you see why?
