3.1 Doing some doing and undoing
Now you’ve had a look at an example, see how you get on with the next activity.
Activity _unit5.3.1 Activity 7 Working out the number
Try to work out what number was thought of in the following problems. You may find it helpful to use some doing-undoing diagrams to visualise, and keep track of these.
- a.Think of a number, subtract 3, and the answer is 2.
Answer
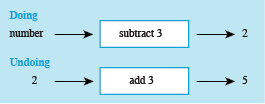
So, the initial number was 5.
Remember, you can check your answer by using it with the instruction to check you obtain the correct answer given. So, 5 − 3 = 2!
- b.Think of a number, multiply by 5, and the answer is 35.
Answer
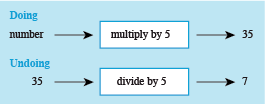
So, the initial number was 7. (Check 7 × 5 = 35).
c.Think of a number, add 4, double it, and the answer is 14.
Click on ‘reveal comment’ if you would like a hint
Discussion
When you have to deal with more than one operation, just take each step in turn. Write down the doing diagram and draw the undoing one underneath, working backwards to undo each operation.
Answer
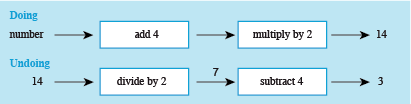
So, working from the left in the undoing diagram, 14 ÷ 2 = 7 and 7 − 4 = 3.
If you like, you can write the output from each box on the arrow as shown in Figure 13 above.
So, the initial number was 3. (Check: 3 + 4 = 7, then 7 × 2 = 14).
- d.Think of a number, add 5, multiply by 3 and subtract 4. The answer is 17.
Answer
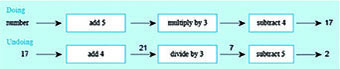
So, if the answer is 17, undoing the steps by working from right to left gives:
| Instruction | Expression |
|---|---|
| Add 4 | |
| Divide by 3 | |
| Subtract 5 |
So, the initial number was 2 this time. (Check: 2 + 5 = 7, then 7 × 3 = 21 and 21 − 4 = 17).
You may be wondering what is the point of all this doing/undoing business! Sometimes there is a need to change a formula so that you can work out something different from it. This is called rearranging the formula and does occur quite frequently in any subject area that uses formulas. The same technique that you have been looking at in this section on ‘undoing’ instructions can be used when rearranging formulas, as you’ll see in the next section.
