3.1 Formulas for areas
Many areas can be built out of basic shapes such as rectangles, triangles or circles, and these areas can be calculated using formulas. For example, if a rectangular room measures 4 m by 3 m and you are covering it in carpet tiles that are each 1 m square, the tiles can be arranged in three rows, each with four tiles. So the total number of tiles will be 3 x 4 = 12 and the area covered is written as 12 m2.
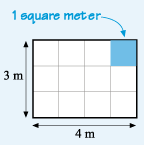
This area could have been calculated directly, without the need for squares, by multiplying the length of the room by its width. Provided both measurements are in the same units, the following formula holds for any rectangle (including a square):
From the formula for the area of a rectangle, the formulas for the area of a parallelogram and a triangle can be derived. Starting with a parallelogram, cut off the left edge and place it next to the right edge to make a rectangle, as in Figure 20. This must have the same area as the parallelogram, as nothing has been added or taken away.
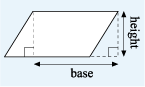
The area of the rectangle can be found by multiplying its length by its height. In the case of a parallelogram, the length is called the base and the width the height. This gives the formula:
Now if this parallelogram is cut in half along a diagonal, this gives two possibilities, as illustrated in Figure 21:
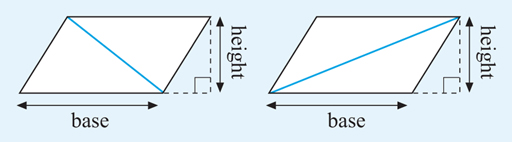
In each case, the parallelogram has been split into two triangles that are each half the area of the parallelogram.
This then gives a general formula for the area of a triangle:
The height goes through the vertex (the point where two lines meet) that is opposite, the base and is always perpendicular, to the base, as shown in Figure 22:
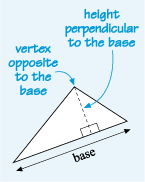
You’ll look at an example in the next section before having a go yourself.
