3.3 Areas of circles
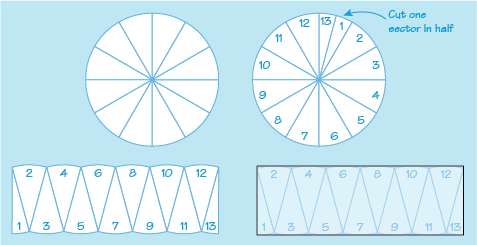
You can show that the area of a circle is calculated by multiplying the square of the radius by , by splitting the circle into equal sized segments and then arranging these to form a rectangle as shown in Figure 25:
If each segment is made gradually smaller, any ‘bumps’ along the top and bottom edges will be smoothed out to form a line that is closer and closer to being straight. The height of the rectangle will then be the same as the radius of the circle and the length half of the circumference. The area of this rectangle will therefore be equivalent to that of the circle.
The
The circumference and radius are related by the following formula:
So
So putting this together gives:
The formula for the area of a circle is therefore:
If you are given the diameter of a circle instead of the radius, the first step to take when working out the area would be to halve the diameter.
See how you get on with applying this new formula in the next activity.
Activity 7 Everyday structures
Calculate the areas of the following road and town developments, assuming that the measurements are sufficiently accurate to allow answers to the nearest whole number. Remember to click on ‘reveal comment’ for a hint or tip.
- a.A roundabout of radius 15.6 m.
Answer
a.
- b.A circular building with a diameter of 54 metres.
Comment
Remember that you need the radius, not the diameter for the formula for area of a circle.
Answer
b.Here you are given the diameter. The radius is half the diameter.
- c.A semicircular lecture hall with a diameter of 46 m.
Answer
c.The area of a semicircle is half the area of a circle.
So the
The lecture hall has a diameter of 46 m so the radius is 23 m.
The last few sections have included a number of different formulas, so you might appreciate a quick summary to bring them altogether. You might also like to take a note of them alongside any new vocabulary you’ve come across
From your study of measurement in Week’s 1 and 2 of the course you will know that there is one final property of shapes that hasn’t been covered, that is capacity or volume. So, you’ll move onto that now in the final part of this week’s study.