1 The physical principles of wave energy

Ocean waves are generated by wind passing over long stretches of water known as ‘fetches’. Three main processes are involved:

1. Air flowing over the sea exerts a tangential stress on the water surface, resulting in the formation and growth of waves.
2. Turbulent air flow close to the water surface creates rapidly varying shear stresses and pressure fluctuations. Where these oscillations are in phase with existing waves, further wave development occurs.
3. Finally, when waves have reached a certain size, the wind can exert a stronger force on the upwind face of the wave, causing additional wave growth.

Because, as we saw in Week 6, the wind is originally derived from solar energy we may consider the energy in ocean waves to be a stored, moderately high-density form of solar energy. Solar power levels, typically of the order of 100 W m^–2 (mean value) can be eventually transformed into waves with power levels of up to 30 kW per metre of crest length.

This measure of wave power is used because the nature of waves makes it impossible to refer to power per unit area: we have to consider that the wave action takes place throughout the depth of water, and so we consider the power passing through a one metre wide slice of water.

Maximise

Figure 1 Characteristics of an idealised wave

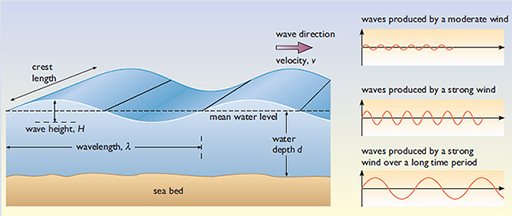
Let’s start by looking at an idealised wave as shown in Figure 1.

This simple, ‘regular’ wave can be characterised by:

• its wavelength (λ) – the distance between successive peaks (or troughs) of the wave,
• its height (H) – the difference in height between peaks and troughs, and
• its period (t) – the time in seconds taken for successive peaks (or troughs) to pass a given fixed point.

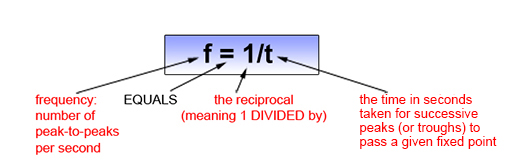
The peaks and troughs of the wave move across the sea surface with a velocity (v) and a frequency (f) – the number of peak-to-peak (or trough-to-trough) oscillations of the wave surface per second. Mathematically, the frequency f is the reciprocal of the period, as shown in Figure 2.

Maximise

Figure 2 The frequency of a wave is equal to the reciprocal of its period

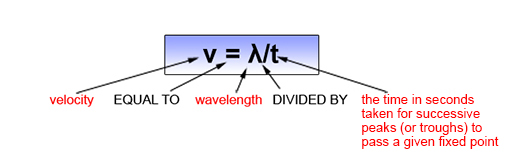
So if a wave is travelling at velocity v past a given fixed point, it will travel a distance equal to its wavelength in a time equal to the wave period t. This can be expressed in the equation in Figure 3.

Maximise

Figure 3 Wave velocity equals wavelength divided by its period

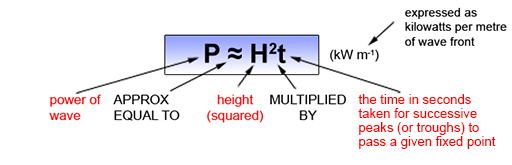
It can be shown that the power, P, of an idealised ocean wave is approximately equal to the square of its height, H (in metres), multiplied by the wave period, t (in seconds). P can be expressed (approximately) in kW per metre of wave front, in the equation shown in Figure 4.

Maximise

Figure 4 Wave power approximately equals height squared times period

There are differences between waves in deep and shallow water, which you will look at next.