5 Percentages
Like fractions and decimals, you’ll see plenty of references to percentages in your everyday life. For example:
This section will help you to:
- order and compare percentages
- work out percentages in different ways
- understand how percentages increase and decrease
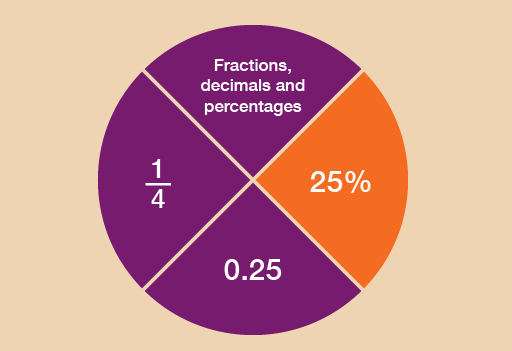
- recognise common equivalencies between percentages, fractions and decimals.
So what is a percentage?
- It’s a number out of 100.
- 40% means ‘40 out of every 100’.
- The symbol for percentage is %.
- 100% means 100 out of 100. You could also say this as the fraction .
You may have seen examples of percentages on clothes labels. ‘100% wool’ means that the garment is made entirely of wool and nothing else. ‘50% wool’ means that the garment is half made of wool, half made of other materials.
The following example shows how to work out the percentage discount.
Example: How can you calculate percentage reductions?
An online shop offers a 10% discount on a television that usually costs £400. How much discount do you get?
There are different ways that percentages can be worked out. The method that you choose really depends on the numbers that you are working with.
Here are two methods for solving this problem:
Method 1
A percentage is a number out of 100, so 10% means ‘10 out of 100’. This could also be put as , or 10 hundredths.
Just like fractions, we start with finding 1%.
If we first work out of £400, we can then work out of of £400. To find of £400:
400 ÷ 100 = 4
So 10/100 of £400 is:
4 × 10 = 40
The discount is £40.
If you think of 10% as a large fraction, , you use the rule of dividing by the denominator (the bottom number in a fraction) and multiplying by the numerator (the top number).
There is an alternative method for finding the answer.
Method 2
A percentage is a number out of 100, so 10% is , which is the same as saying .
If we want to find out 10% of £400, that’s the same as finding out of £400:
400 ÷ 10 = 40
This gives us the answer £40.
Which method do you prefer?
- Method 1 will always work.
- Method 2 can be used to work out percentages in your head if the numbers are suitable.
If you want to use Method 2, here are some common percentages given in fraction form:
10% =
25% =
50% =
75% =
If you want to know what 20% of a number is, work out 10% and multiply the answer by 2.
Similarly, if you want to know what 30% is, work out 10% and multiply the answer by 3.
If you need to know 5%, work out 10% and then halve the answer.
Use the example above to help you with the following activities. Remember to check your answers once you have completed the questions.
Activity 14: A holiday discount
You need to pay a 20% deposit on a holiday that costs £800. How much is the deposit?
Answer
Method 1
In order to identify how much the deposit is, you need to find out what 20% () of £800 is. To do this, first you need to find out of £800:
- 800 ÷ 100 = 8
So of £800 is:
- 8 × 20 = 160
The deposit is £160.
Method 2
In order to calulate 10%, or , you need to divide the number by 10:
- 800 ÷ 10 = 80
You now have 10% and you need 20%. Therefore you need to multiply your 10% by 2:
- 80 × 2 = 160
The deposit is £160.
Activity 15: Comparing discounts
The same diamond ring is being sold at different prices, and with different percentage discounts, in two different shops.
Which shop offers the better deal?
Please check your answers before you move on.
Answer
In order to identify Shop A’s discount, you need to find out what 25% () of £500 is. To do this, first you need to find out of £500:
- 500 ÷ 100 = 5
So of £500 is:
- 5 × 25 = 125
The discount is £125, so you would have to pay:
- £500 – £125 = £375
In order to identify Shop B’s discount, you need to find out what 10% () of £400 is. To do this, first you need to find out of £400:
- 400 ÷ 100 = 4
So of £400 is:
- 4 × 10 = 40
The discount is £40, so you would have to pay:
- £400 – £40 = £360
So Shop B offers the best deal.