3.2 Formal written methods for subtraction
Subtraction is experienced as being more difficult than addition. Subtraction is the inverse of addition and knowing this can help learners to use complementary addition in informal methods of subtraction.
Video 4 demonstrates the decomposition method (or column method) of subtraction and the empty number line method which uses complementary addition. This latter method is a visible example instantiation of the method which many people use mentally.
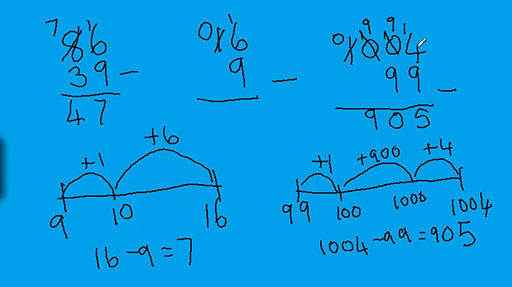
Transcript: Video 4 Choosing the best method for subtraction
Activity 8 Choosing the most appropriate method of subtraction
Consider the following subtractions and decide whether it is more appropriate to use the decomposition method or the empty number line method.
- a.
- b.
c.The length of a journey which starts at 9.55 a.m. and ends at 11.05 a.m.
Discussion
If the numbers in the subtraction are close together then it makes more sense to ‘count up’ from the smaller to the larger, the method known as known as complementary addition. This is especially useful if the numbers bridge over a 10s or 100s sort of number or over the hour in a time calculation.
