3.1 Calculating percentages of amounts
When calculating a percentage of an amount, many learners reach for the method of putting the percentage over one hundred and multiplying by the amount over one. As an example, 35% of 60 is calculated below using this method.
This method works if you are good at arithmetic and can remember the procedure! However, it is more intuitive to use some common knowledge: that 10% is equivalent to one-tenth, 1% is equivalent to one-hundredth, 50% is equivalent to one-half, and 25% is equivalent to one-quarter. Other percentages can be worked out from these.
The mathematical cake, which you met in Section 1 on equivalence between fractions, decimals and percentages, also proves useful in helping younger learners to understand the concept of percentages of amounts. It can be used to find multiples of 10% of amounts by imagining the cake cut into ten slices as before. Watch Video 4 to find out about a useful approach to working out percentages of an amount.
Transcript: Video 4 Using the mathematical cake diagram to find percentages of an amount
Answer
Once learners have been introduced to the mathematical cake diagram, they will certainly be familiar with finding 10% of an amount and multiples of 10% of an amount. It is also intuitive to find 25% and 50%.
For example, 35% of 60 can be found by doing the following:
- (multiplying 10% of 60 by 3)
- (finding half of 10% of 60)
- (adding the results of finding 30% and 5%)
Activity 9 Find percentages of 60
A useful exercise to do with your learners is to ask them what percentages of 60 they can find, encouraging them to modify the methods they have previously used for finding simple percentages of amounts. Try this one yourself (Figure 4).
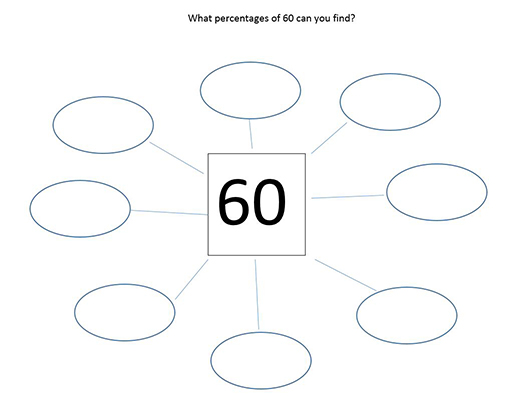
Discussion
There are many possible questions and answers that you could have posed in the diagram.
Examples could be 50% of 60, 30% of 60, or 25% of 60.
Extend learners’ understanding by posing questions such as: 15% of 60, how could you find that? What about 76% of 60? Or 120% of 60?
Ask learners to pose ‘What percentage of 60?’ questions themselves.
So far, if your learners have been using the methods shown above, they will have found percentages of amounts by making reference to the equivalent fractions.
Decimal equivalents can also be used when calculating percentages of amounts and this is a more helpful form when using a calculator. Referring back to the mathematical cake diagram in Section 1.1, remember that etc.
To convert from percentages to decimals, the percentage has been divided by 100. This follows from an earlier observation about fractions, which stated an alternative meaning of the numerator and denominator, i.e. numerator divided by denominator. In other words:
For example, if calculating 76% of 60, the learner keys into the calculator:
However, it becomes easy to convert 76% straight away to 0.76 and then multiply by 60.
It is worth raising a caution here about using the percentage button on a calculator. Since the percentage button functions in different ways on different makes of calculator , it is best not to use it. Instead, encourage learners to convert the percentage to a decimal and then multiply by the amount.
