1 Function machines
The function machine is a way of thinking about three aspects that make up a function: the inputs, the outputs and the rule that determines their connection (Figure 2). The representation as a machine connects them in one diagram (just like seeing a toaster makes you think of bread and toast).
You have already seen examples of such thinking in the ‘Think of a Number’ problems. The input is the number you think of, you calculate given a rule and you tell someone the answer – the output.
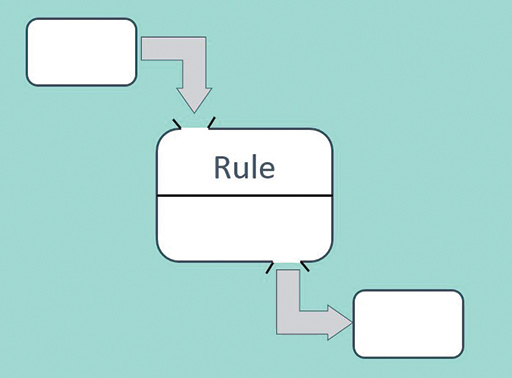
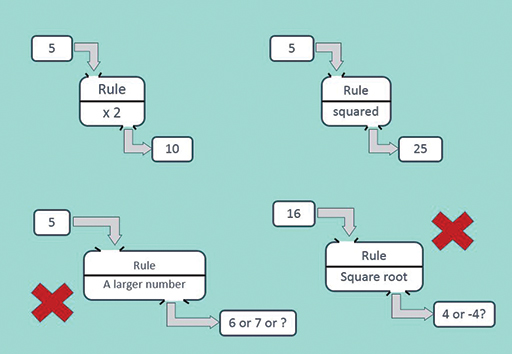
The rules for functions can be as simple as ‘double’ or ‘stay the same’ and as complicated as you like. (It does not even have to be expressed in symbols.) The rule does have to be ‘well defined’, meaning that for each input number there is only one possible answer.
This condition means that two of the examples in Figure 3 are not functions:
As you saw with Think of a Number problems, the function machine representation is powerful because learners can work with it at the level of taking a specific unknown quantity – the input – and calculating with it to get an output. In this sense, the function is a process that they can carry out.
The machine representation also lends itself to more sophisticated tasks requiring learners to go beyond simply finding outputs. Teachers can introduce the idea of the input as a quantity that can take any value. They can set tasks where the process of writing and comparing the rules and outputs is more important than what numbers they are. The two activities you will carry out in this section illustrate this kind of task.
The goal of working in this way is laying the foundations for learners to treat quantities as variables and to use functions fluently in later mathematics.
For example:
- the squaring function is used in finding the area of a circle
- the cubing function is used in finding volume
- the sine function is used in trigonometry (and, of course, the cosine and tangent functions).
The ‘machine’ analogy suits these examples since it corresponds to learners’ experiences of pressing the calculator key for that function (Figure 4). Before calculator technology, all of these functions were either calculated or looked up in special booklets of tables.

Activity 1 Getting used to long expressions
On a piece of paper, write an expression that summarises the following sequence of functions.
Think of a number, then:
- add 3
- multiply by 2
- subtract 5
- divide by 3
- add 72
- multiply by 6.
Then watch the video below from the OU archives. It introduces a teacher, and shows him building up the sequence with 14-year-old learners on a board. Ask yourself:
What do you think the teacher’s learning objectives are?
How do learners react to calculating on an unknown quantity?
What does the teacher do to draw attention to conventional symbol use?

Transcript: Video 1 Working mathematically with symbols at Key Stage 3
Discussion
The emphasis of the video activity is on gaining familiarity with symbols to express the whole sequence without any intermediate results being calculated. Note how the teacher builds up the expression first by ‘doing’ each function, and then by ‘undoing’ it. ‘Doing and undoing’ is an important idea in algebra. It provides an organising structure to relate processes that appear different but are the reverse of each other, such as × and ÷. This allows us to reduce the complexity of calculations.
The next activity is a well-tested teaching approach devised by Don Steward, called ‘both ways’. Using two functions (× 2 and + 3) increases the level of complexity, and going both ways allows learners to make predictions about the results. This task is designed to shift attention from calculating outputs towards comparing methods of calculation. The activity is written in the way you would use it with a class of learners, although you would need to offer support for some of the calculations (for example, a negative number line).
Activity 2 Both ways
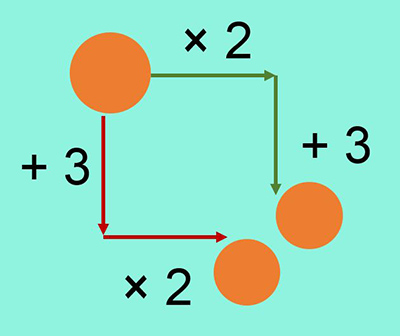
You are going to choose an input number and follow the instructions on the arrows in Figure 5 – both ways. Do you think your answers will be the same?
- Try starting with these numbers: 5, 8, 3.1, –4, 100, 1000
- a million (you could write m for short)
- a billion (b for short)
- any number (n for short)
- Compare the two answers you get. Can you explain what is happening?
Discussion
You get different answers by going different ways:
13 (green way) and 16 (red way), 19 and 22, 9.2 and 12.2, –5 and –2, 203 and 206, 2m+3 and 2m+6, etc.
The difference between the answers is always 3, for any input number.
Using m for a million, etc. is a popular way of introducing letters for numbers in function machines. It matches the way we speak about such numbers in words: 2 million and 3. It is mathematically correct in that m, b, t all stand for numbers – one million, one billion, etc. – rather than objects such as mangos or bananas that cannot be calculated with.
Although it is a good introduction, it is not an approach to stay with. (For example, you do not want learners to write 2 million one hundred and three as 2m1h+ 3 or think that m always stands for a million.) This is why the sequence of examples ends with using n for ‘any number’ (the sound rhyme helps learners accept this meaning).
You could explain this result with diagrams using a rectangle for n and dots for each 1. The important step is that, following the red arrows, both the number and the 3 dots get multiplied by 2.
This activity shows the need to use brackets when you combine addition and multiplication in a single expression. If you are confident with algebra, you might have explained it to yourself by writing the expression for each way and expanding the brackets. However, learners in middle school are unlikely to be convinced by manipulating symbols because they do not yet feel concrete to them.
green arrows 2n+3
red arrows 2(n+3) = 2 × n + 2 × 3 = 2n + 6
2n and 2n are the same number, but 6 is more than 3 so the difference is 3.
You can find resources related to this activity on the Median blog at https://donsteward.blogspot.com/ [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] indexed under ‘Expressions Both Ways’.
