Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Electromagnetism: testing Coulomb’s law
Electromagnetism: testing Coulomb’s law

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

3 Testing Coulomb’s law and using vector components

This activity has three parts: a video demonstration of an experiment, an exercise and a video solution. The activity gives you a practical demonstration of electrostatic forces and the opportunity to practise using the vector form of Coulomb’s law. It also encourages you to think about the assumptions in your calculations and possible sources of experimental uncertainty.

Activity icon

Activity Testing Coulomb’s law and using vector components

Timing: Allow up to 1 hour

Part 1 Measuring electrostatic forces

Watch Video 1, which shows Open University (OU) academics Sam Eden and Anita Dawes measuring one component of the electrostatic force that a charged sphere feels due to nearby charged spheres.

Download this video clip.Video player: Video 1
Copy this transcript to the clipboard
Print this transcript
Show transcript | Hide transcript

Transcript: Video 1 Filmed experiment: measuring electrostatic forces at the OU.

[Text on screen: Sam Eden, Physicist, The Open University]
SAM EDEN
In this activity, we are going to carry out experiments with the aim of answering two main questions. Firstly, does Coulomb’s law give you the correct electrostatic force that a charged sphere feels due to one other charged sphere? And secondly, does adding vector components give you the correct electrostatic force that a charged sphere feels due to two other charged spheres?
After you’ve watched the experiments, you will analyse the results and compare them with your own calculations using vector components. Now, let’s start with a quick tour of the experiment.
[Text on screen: Anita Dawes, Physicist, The Open University]
ANITA DAWES
OK, so the experiment involves measuring one vector component of the force that a charged sphere feels after we have positioned another charged sphere, or two charged spheres, nearby. So here’s one of the spheres. So it’s a hollow conducting sphere mounted on an insulating plastic rod.
And what we’ve done here is prepared a Perspex system to help us place our spheres in precise positions above a grid. So on this grid, each square is two centimetres by two centimetres. Now, here’s our sphere that we used as a test charge. It’s mounted on an arm with a pressure sensor that’s very sensitive. We can measure the force that it feels between the charges in this direction, perpendicular to the arm.
[In a top-down view of the experiment, sphere A is positioned to the left of the test charge sphere. An arrow labelled ‘Fx’ pointing to the right, away from the test charge, is superimposed on the screen.]
Each time we’re ready to take a measurement of the force, this sensor is connected to this unit here, and we can save a series of values at 20-millisecond intervals. Now let’s talk about the system that we use for charging up the spheres.
SAM EDEN
So this is a power supply with a pin that you can touch onto the spheres to transfer a charge onto them. We’ve put the power supply quite far from the rest of the experiment as part of our effort to minimise external electric fields. The power supply’s been calibrated, so we know that a voltage of 17 kilovolts transfers 30 nanocoulombs onto a sphere. So now we’re ready to start the experiments.
ANITA DAWES
Here’s our first arrangement of the test charge sphere and the other sphere, which we’ll call sphere A. The centres of the spheres are ten centimetres away from each other.
[A distance marker labelled ‘10.0 cm’ is superimposed on a top-down view of the experiment, and is positioned between the test charge sphere and sphere A.]
So first, we’ll record the force on the test charge sphere before we put any charge on the spheres. So I’ll take the readings now.
And you should see the last six force readings on your screen that have been saved by this readout. The readings in millinewtons are minus 0.05, minus 0.05, minus 0.07, minus 0.05, minus 0.07 and minus 0.06. You’ll be able to access all the data from these experiments after you’ve watched this video.
So what we’ll do next is put 30 nanocoulombs of charge on the test charge and on sphere A. Now I’ll record the readings, and you should see them appear on your screen. The values in millinewtons are 0.62, 0.63, 0.65, 0.64, 0.68 and 0.69.
Now we’ll ground these two spheres. So I’ll use an earth rod and touch them to take the charge away. And we’ll add a third sphere into the geometry. And I’ll place it into this position here.
[In a top-down view of the experiment, sphere B is positioned above the test charge sphere. The lines from the test charge sphere to spheres A and B are both labelled as ‘10 cm’ and are at right angles to each other.]
Once again, we’ll check the force without any charge on it. The values in millinewtons are minus 0.08, minus 0.09, minus 0.11, minus 0.12, minus 0.11 and minus 0.10.
And we’ll now put 30 nanocoulombs of charge on all three of the spheres. Once again, you will be able to see the values on the screen. The values in millinewtons are 0.65, 0.64, 0.64, 0.65, 0.67 and 0.68.
Don’t forget that we’re only measuring one component of the force on the test charge. So now we’ll ground the three spheres again. And I will move sphere B into a new position, here.
[In a top-down view of the experiment, sphere B is positioned above sphere A. The lines from sphere A to the test charge sphere and sphere B are both labelled as ‘10 cm’ and are at right angles to each other.]
And now once again, we’ll check the force without any charge applied to the spheres. So I’ll make the measurement.
The values in millinewtons are minus 0.04, minus 0.05, minus 0.06, minus 0.05, minus 0.07 and minus 0.07. And now we’ll put 30 nanocoulombs on all three spheres. We’ll take another measurement. The values in millinewtons are 0.98, 0.99, 0.99, 0.99, 0.98 and 1.00. And that completes our measurements.
SAM EDEN
You will find the data that we’ve just recorded in the next part of the activity. You will then do your own calculations to test if Coulomb’s law combined with vector addition predicts these experimental results with good accuracy.
End transcript: Video 1 Filmed experiment: measuring electrostatic forces at the OU.
Download
Video 1 Filmed experiment: measuring electrostatic forces at the OU.
Interactive feature not available in single page view (see it in standard view).

(The data shown on-screen during Video 1 are available in an Appendix to this activity.)

Part 2 Calculating electrostatic force components and comparing them with the measured values

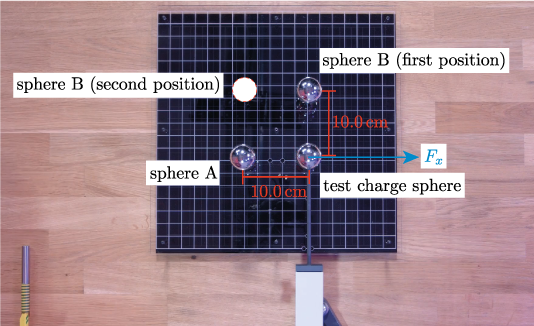
Figure 1 shows the x -direction and the relative positions of the charged spheres in the filmed experiment.

Described image
Figure 6 Annotated still image from Video 1 showing the positions of the test charge sphere, sphere A, and two possible positions for sphere B, as well as the force component cap f sub x .
Show description|Hide description

The centre of sphere A is placed at a horizontal distance of 10.0 centimeters to the left of the centre of the test charge sphere. The centre of sphere B (first position) is placed at a vertical distance of 10.0 centimeters above the centre of the test charge. The centre of sphere B (second position) is placed at a horizontal distance of 10.0 centimeters to the left of the centre of sphere B (first position). A force arrow labelled F subscript x from the test charge points horizontally to the right.

Figure 6 Annotated still image from Video 1 showing the positions of the test charge sphere, sphere A, and two possible positions for ...

(a)

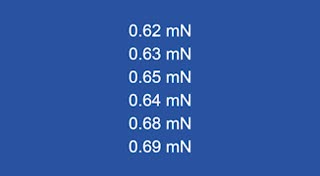
Use the vector form of Coulomb’s law to predict the x -component cap f sub x of the force that the test charge sphere feels in the three situations described below. All charges are given in units of nanocoloumbs ( nC ). Write your answers in millinewtons ( mN ) in Table 1.

  • i.The test charge sphere and sphere A are charged with 30 nC each. Sphere B is not present.
  • ii.The three spheres are charged with 30 nC each. Sphere B is in its first position (see Figure 1).
  • iii.The three spheres are charged with 30 nC each. Sphere B is in its second position (see Figure 1).
Table 1 Calculated force on the test charge.
situation calculated cap f sub x postfix solidus mN
i
To use this interactive functionality a free OU account is required. Sign in or register.
ii
To use this interactive functionality a free OU account is required. Sign in or register.
iii
To use this interactive functionality a free OU account is required. Sign in or register.
Words: 0
Interactive feature not available in single page view (see it in standard view).

(b)

Comment briefly on possible reasons why your calculated cap f sub x values may not agree exactly with the experimental values. Consider approximations in your calculations and experimental uncertainties that may have significant effects.

To use this interactive functionality a free OU account is required. Sign in or register.
Interactive feature not available in single page view (see it in standard view).

Discussion

Keep in mind that the discussion below only addresses a selection of issues; there are various other valid points that you might have raised in your answers.

The key assumption in the calculation is that the charged spheres can be treated as point charges located at the spheres’ centres. At any position outside a spherically symmetric charge distribution, the field produced by the charge distribution is the same as the field that would be produced by a point charge located at its centre. This is a consequence of Gauss’s law (one of the four key laws in electromagnetism known as Maxwell’s equations). However, in this experiment the charge distribution around each sphere will not be perfectly spherically symmetric. This is partly because no manufactured sphere is perfect, but a more fundamental issue is that the electric field produced by one charged sphere will disrupt the spherical symmetry of the charge distribution on another.

Testing the experiment before filming indicated that most significant sources of experimental uncertainty were unwanted forces and charge leakage, as described below.

The test charge sphere can experience unwanted forces (that is, forces other than the electrostatic force due to nearby charged spheres). For example, air flow in the studio and vibrations transmitted from the floor had noticeable effects in the tests before filming.

Charge leakage occurs in the time between charging the spheres and measuring the forces. No insulator is perfect, and the rate at which charge dissipates from the spheres is sensitive to factors such as air humidity and the cleanliness of the plastic rods.

Further sources of experimental uncertainty include:

  • The charge transferred to each sphere is known to a limited precision. This depends on the calibration procedure.
  • No force meter is perfectly accurate, and the measured forces are displayed to a limited precision.
  • Video 1 does not provide information on how precisely the test charge sphere has been positioned to measure the x -component of the force that it feels.
  • The x - and y -positions of the spheres’ centres are given to a limited precision, and the video does not provide information about precisely how they are situated on the x times y -plane.

Part 3 Applying the vector form of Coulomb’s law – a model solution and discussion of the results

(a)

Watch Video 2 in which Sam presents model solutions for the three situations described in Part 2(a) of this activity. The video highlights the use of use of displacement vectors, position vectors, unit vectors and vector components.

Download this video clip.Video player: Video 2
Copy this transcript to the clipboard
Print this transcript
Show transcript | Hide transcript

Transcript: Video 2 Using the vector form of Coulomb’s law to determine theoretical force components for comparison with the measurements in Video 1.

[Text on screen: Using the vector form of Coulomb’s law to calculate electric forces on charged spheres]
SAM EDEN
SAM EDEN: In this screencast, we’re going to use the vector form of Coulomb’s law to calculate the forces between the charged spheres in our filmed experiments. So let’s start by sketching the experiment. We’ll assume that we can treat the charge spheres as point charges. So here’s our test charge T. And we’ll place it at the origin of a set of Cartesian coordinates. All our charges are on the xy-plane so we can treat this as a two-dimensional problem.
Charge A is at (minus 0.100 metres, 0.000 metres). I’m giving the coordinates to three significant figures in agreement with the experiment video. And the third charge can be at B, which is (0.000 metres, 0.100 metres). Or at B′, which is (minus 0.100 metres, 0.100 metres). Finally, our sensor measures Fx, which is the x-component of any force that the test charge feels.
Now let’s write down the vector form of Coulomb’s law. The force on point charge 1 due to point charge 2 is written F12. And this is equal to a constant, kelec, which is 1 over (4πε0), multiplied by the charges q1 and q2, divided by the magnitude of the displacement vector r12 squared. And the direction of the force is given by the unit vector r12 hat.
Remember that r12 is the vector from point 2 to point 1. And we can express this as the magnitude r12 multiplied by the unit vector, r12 hat, which is equal to the position vector of point 1, r1, minus the position vector of point 2, r2.
OK, so our first situation has 30 nanocoulombs at T and at A. Let’s start by working out our displacement vector from A to T.
rTA [times] rTA hat equals the position vector rT, minus the position vector rA, which is (xT minus xA) ex plus (yT minus yA) ey.
Now we can substitute in our coordinates for T and A to give us (0 minus (minus 0.100 metres)) ex plus (0 minus 0.000 metres) ey, which is 0.100 metres times the unit vector ex. So the magnitude rTA is 0.100 metres. And rTA hat is ex. Now you may have recognised this without needing to subtract the position vector rA from rT, but working through this in full is good practice for situations with more complicated geometry.
So if we substitute the magnitude rTA and rTA hat into Coulomb’s law, we get FTA equals kelec times q1 q2, which is (30 times 10 to the minus 9 coulombs) squared, divided by (0.100 metres) squared, all multiplied by ex. And then crunching the numbers gives us 0.81 millinewtons ex.
Now on to our second situation. It’s the same as what we just looked at, except we’ve added a third sphere with 30 nanocoulombs at position B. Due to the principle of superposition of electric fields, the total force on T must be the sum of the forces due to the charges at A and B. So we need FTB. We can apply the method you just saw, but it’s quicker to work this out using symmetry.
If you rotate the charge at A 90 degrees clockwise about T, then it ends up at position B. So FTB must be FTA rotated 90 degrees clockwise. So the vector FTB equals the magnitude FTA multiplied by minus ey. And this means that FTA plus FTB equals 0.81 millinewtons ex, that we worked out just a moment ago, minus 0.81 millinewtons ey.
Now in our third situation, we have 30 nanocoulombs at T, A and B′. So we need the force FTB′ and we’ll add this to FTA. Let’s work out our displacement vector from B′ to T. That’s the position vector rT minus the position vector rB′, which is (0 minus (minus 0.100 metres)) ex plus (0 minus 0.100 metres) ey. And that equals 0.100 metres (ex minus ey).
Now we need the magnitude of rTB′. And we can work that out by drawing a right-angle triangle like this and then using Pythagoras’ theorem. So the magnitude rTB prime is the square root of (0.100 metres squared plus 0.100 metres squared), which is root (0.0200 metres squared). Now from the definition above we know that rTB′ hat is the vector rTB′ over the magnitude rTB′.
So let’s substitute this expression for rTB′ hat into Coulomb’s law. And we get FTB prime equals kelec times (30 times 10 to the minus 9 coulombs) squared, times the vector rTB′, which is 0.100 metres (ex minus ey), divided by the magnitude rTB′ cubed, which is (0.0200 metres squared) to the power of 3 over 2. And this comes to 0.29 millinewtons (ex minus ey).
Now we can add up FTA and FTB′ to get 0.81 millinewtons ex plus 0.29 millinewtons (ex minus ey), which is 1.1 millinewtons ex minus 0.29 millinewtons ey, keeping everything to two significant figures in line with the precision of our charge values. So our calculated Fx is 1.1 millinewtons.
So now we’ve used vector components to calculate the force that acts on the test charge in each of the three situations in the experiment video.
End transcript: Video 2 Using the vector form of Coulomb’s law to determine theoretical force components for comparison with the measurements in Video 1.
Download
Video 2 Using the vector form of Coulomb’s law to determine theoretical force components for comparison with the measurements in Video 1.
Interactive feature not available in single page view (see it in standard view).

The experimental results from Video 1 are summarised in Table 2 for the three situations described in Part 2(a). In each situation, cap f sub x was recorded in mN before and after the spheres were charged. The results from Video 2 are also shown and your calculated values from Table 1 are also shown [please refresh the page if calculated values from Table 1 haven’t populated the boxes in the last column].

Table 2 Summary of the results from Videos 1 and 2.
situation average measured cap f sub x postfix solidus mN calculated cap f sub x postfix solidus mN values from Video 2 your calculated cap f sub x postfix solidus mN values from Table 1
uncharged charged difference
i –0.058 0.65 0.71 0.81
To use this interactive functionality a free OU account is required. Sign in or register.
Original location 1
ii –0.10 0.66 0.76 0.81
To use this interactive functionality a free OU account is required. Sign in or register.
Original location 2
iii –0.057 0.99 1.0 1.1
To use this interactive functionality a free OU account is required. Sign in or register.
Original location 3

(b)

Compare the calculated cap f sub x values in Table 2 with the experimental results (in the ‘difference’ column). Does this comparison support the validity of Coulomb’s law and of your method for applying it in situations with more than two charges?

To use this interactive functionality a free OU account is required. Sign in or register.
Interactive feature not available in single page view (see it in standard view).

Discussion

For brevity, this discussion is limited to the point charge assumption, and the effects of charge leakage and unwanted forces.

Point charge assumption

The field produced by one charged sphere disrupts the spherical symmetry of the charge distribution on another. This causes the concentration of positive charge to be greatest on the side of each sphere that is furthest from the other positively charged spheres. Hence, treating the charged spheres as point charges located at the spheres’ centres represents an underestimation of the separation of the charge distributions on each sphere.

Charge leakage

Charge leakage occurs during the time between charging the spheres and measuring the forces. This means that the magnitude of the charge on each sphere at the instant that the force is measured is lower than the 30 nC that was initially transferred.

It follows that the point charge assumption and charge leakage both cause the calculated forces to be higher than the forces in the experiment. This is broadly consistent with Table 2, where calculated forces are between 6% and 12% higher than the experimental values.

Unwanted forces

Table 2 shows that force measurements prior to charging the spheres vary over a range of 0.04 mN . This provides a first approximation for the variation in the unwanted forces. The variation is close to the difference between the cap f sub x values measured in situations (i) and (ii), which the calculations indicate should be the same.

Summary

This short discussion indicates that the key approximation in the calculation and the main sources of experimental uncertainty are broadly consistent with the differences between the calculated and measured forces in this activity. Therefore, the experimental results are broadly supportive of the validity of Coulomb’s law and the present method for applying it in situations with more than two charges.