2.1 Models
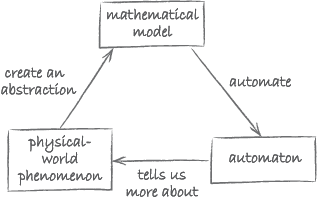
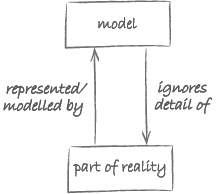
Let us think more generally about the abstraction depicted in Figure 5. For this purpose, we will be using the diagram in Figure 6. Instead of Wing’s somewhat unwieldy expressions ‘mathematical model’ and ‘physical-world phenomenon’, we will use the shorthands ‘model’ and ‘part of reality’.
The diagram in Figure 6 shows that abstraction as modelling can be understood in terms of the relationship between a part of reality and a model which represents the details of interest of this reality. For this reason, models are sometimes also referred to as representations.
For the purpose of the current example, the part of reality that we’re interested in is the paper and ink dictionary of Activity 3. The algorithms in Section 1 for looking up words work with a model of a dictionary as an alphabetically sorted list of headwords, each paired with its definition. The model corresponds to how the data that the algorithm works with are structured. This model captures the essentials (i.e. that the dictionary consists of an alphabetically sorted list of words and their definitions) and ignores certain details (for example, that a physical dictionary is divided into pages of a certain size and has a cover to protect it). In other words, the irrelevant details are not reflected by the structure of the data that the algorithm works with.
Activity 4 Representations
Representations, including paintings and drawings, are models. This is brilliantly illustrated by René Magritte’s famous painting of a pipe with the words ‘Ceci n’est pas une pipe’ (‘This is not a pipe’) underneath (Figure 7). Explain how this painting brings home the point that modelling involves two levels: the abstraction and the reality which the abstraction models.
Discussion
When looking at this painting, my initial thought was: ‘Look, a pipe – why does it say in French that this is not a pipe?’ Then it dawned on me that of course this is indeed not a pipe: it’s merely a painting of a pipe. With this painting, Magritte reminded me that representations usually involve two levels: in this case the painting of a pipe and a real pipe on which the painting is based. The former is an abstraction which ignores some of the properties of actual pipes (for example, that they have a smell, usually of tobacco). Interestingly, the title of this painting is La trahison des images (The Treachery of Images).
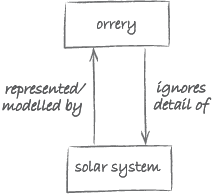
The part of reality for which one creates a model or representation doesn’t need to be a static object such as a pipe or dictionary. It can also be a process or system which changes over time. In that case, the model will not only have to capture any enduring properties of interest, but also any changes in time that are of interest. For example, in astronomy there is a rich tradition of building such models of the solar system (see Figure 8). The purpose of such a model, known as an orrery, is to represent the position of the planets relative to each other over time.
The invention of the orrery is usually attributed to George Graham (1673–1751). Graham worked on this with the support of the 4th Earl of Orrery, which explains the name. The tiny crank on the side of the central cylinder in Figure 8 allows the model to be animated. Turning the crank causes the (representations of the) planets to follow a path around the (representation of the) Sun at the centre of the model. Usually such an animated model is referred to as a simulation.
As with any model, an orrery ignores certain details of the part of reality that it models. For example, compared with the scale of the distances between the planets, the planets are too large. The relationship between the solar system and an orrery is as depicted in Figure 9.