2.5 Computational thinking: the overview diagram
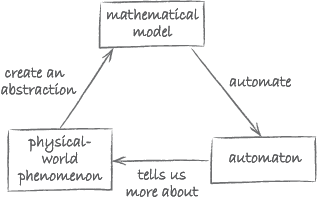
The aim of this subsection is to draw together some of the concepts you have encountered so far. Consider once more the diagram illustrating some of Wing’s ideas (Figure 19).
The three main components in the diagram are:
- a physical-world phenomenon
- a mathematical model
- an automaton.
How do these relate to the concepts you met in Section 1, namely:
- real-world problem
- computational problem
- algorithm and data structures?
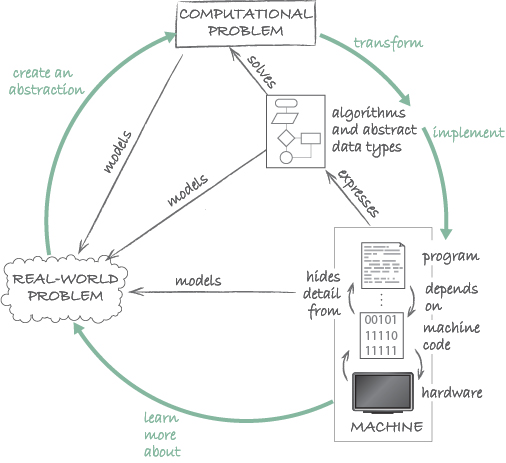
Let us start with Wing’s use of the term ‘mathematical model’. As we will now explain, Wing’s notion of a mathematical model is linked to that of a computational problem. According to Wing, a mathematical model is an abstraction of the physical-world phenomenon of interest. It ignores irrelevant detail. It also is the point of departure for automation. The fact that it is a mathematical model means that it is sufficiently precise to be used as a starting point for creating an automaton. Now, you may recall that we defined a computational problem as a problem that is expressed sufficiently precisely that it is possible to attempt to build an algorithm to solve it. In other words, Wing’s mathematical model is nothing other than a computational problem.
Wing’s physical-world phenomenon is abstracted by the mathematical model, just like a computational problem provides an abstraction of a real-world problem.
Algorithms and data structures form the link between a computational problem and its automation. Finding algorithms and data structures is part of automating. When these are then implemented as a program and executed, they provide a machine that solves the problem. In Wing’s words, the resulting machine – or automaton – automates the abstraction.
The complexity of the machine, as we have just discussed, is managed by having a series of encapsulated layers.
To sum all this up, we can refine the diagram of Figure 19 as shown in Figure 20.
Whereas the core of this diagram represents artefacts (real-world and computational problems, machines) and their relations (models, solves, and expresses), the green arrows indicate the actions that a computational thinker engages in (i.e. create, transform, implement and learn).