5 Napier and Briggs
The fact remains that few mathematical inventions have burst on the world so unexpectedly as Napier’s logarithms. Although various disparate strands – the idea of doing multiplication via addition, the idea of comparing arithmetic and geometric progressions, the use of the concept of motion – had all been floated at some stage, the enthusiasm with which Napier’s work was received makes it clear both that this was perceived as a novel invention and that it fulfilled a pressing need. Foremost among those who welcomed the invention was Henry Briggs, Professor of Geometry at Gresham College, who wrote to the biblical scholar James Ussher in 1615:
Naper, lord of Markinston, hath set my Head and Hands a Work with his new and admirable Logarithms I hope to see him this Summer if it please God, for I never saw Book which pleased me better or made me more wonder.
Note: Ussher was the scholar whose studies of biblical chronology revealed that the Creation took place at 9 a.m. on October 23rd, 4004 BC.
Briggs did indeed ‘see him this Summer’, in a visit recorded some time later by the astrologer William Lilly. See Reading 3 for this famous story.
Reading 3: William Lilly on the meeting of Napier and Briggs
I will acquaint you with one memorable Story related unto me by Mr John Marr, an excellent Mathematician and Geometrician, whom I conceive you remember; he was Servant to King James and Charles the First.
At first, when the Lord Napier, or Marchiston, made public his Logarithms, Mr Briggs, then Reader of the Astronomy lecture at Gresham College in London, was so surprised with Admiration of them, that he could have no Quietness in himself, until he had seen that noble Person the Lord Marchiston, whose only Invention they were; he acquaints John Marr herewith, who went into Scotland before Mr Briggs, purposely to be here when these Two so learned Persons should meet: Mr Briggs appoints a certain Day when to meet at Edinborough, but failing thereof; the Lord Napier were speaking of Mr Briggs: ‘Ah, John (saith Marchiston), Mr Briggs will not now come’; at the very one knocks at the gate; John Marr hasted down, and it proved Mr Briggs, to his great Contentment; he brings Mr Briggs up into My Lord’s chamber, where almost one quarter of an hour was sent, each beholding other almost with Admiration before one word was spoke, at last Mr Briggs began.
‘My Lord, I have undertaken this long Journey purposely to see your Person, and to know by what Engine of Wit or Ingenuity you came first to think of this most excellent Help unto Astronomy, viz., the Logarithms; but, my Lord, being by you found out, I wonder nobody else found it out before, when now known it is so easy,’ He was nobly entertained by the Lord Napier, and every Summer after that, during the Lord’s being alive, this venerable Man, Mr Briggs, went purposely into Scotland to visit him.
During this visit, and a further one the next year (1616), Briggs and Napier discussed some simplifications to the idea and presentation of logarithms. It is fortunate they profited from each other’s company in this way, for their world-views were very different. Napier not only considered the Pope to be the Antichrist and expected the Day of Judgement quite shortly (probably between 1688 and 1700), but also was ‘a great lover of astrology’ (according to Lilly), and may even have practised witchcraft, as contemporary rumour had it. Briggs, on the other hand, represented what one might call the Yorkshire common-sense school of thought on occult matters, and like his friend Sir Henry Savile (also a son of Halifax) had no time for astrological practices.
It was these two very different people who worked together on simplifying logarithms. They agreed it would generally be more useful if the logarithm of 1 were to be 0, and the logarithm of 10 were to be 1 (see Box 2). Briggs spent several subsequent years recalculating the tables on this basis. Thus the early history of logarithms exemplifies well a remark which the historian Clifford Truesdell has made in another context: ‘the simple ideas are the hardest to achieve; simplicity does not come of itself but must be created’ (his full comment is linked below). Napier and Briggs had to work hard to create even the ‘simple’ major logarithm property that
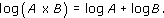
Clifford Truesdell’s full comment was as follows:
Reading 4: Clifford Truesdell on Euler
We may justly wonder that it took more than sixty years for so simple an extension of Newton’s ideas, but the literature of mechanics does not permit us to doubt that it did. As often happens in the history of science, the simple ideas are the hardest to achieve; simplicity does not come of itself but must be created.
Box 2: Napier’s, and later, logarithms
Napier’s original presentation of logarithms differed markedly from that generally adopted later, and it is worth spelling out the differences.
It follows from our earlier description that it was the length PoQ whose logarithm is 0, and further that the shorter the length (in the geometric series) the larger its logarithm. Napier chose P0Q to be 10 000 000, a conventional figure for the ‘whole sine’, because he intended the table of logarithms to be used trigonometrically – it was the logarithms of sines and tangents he calculated and tabulated in the 1614 Descriptio, not the logarithms of numbers in general. A further difference from later practice was that what we think of as the major logarithm property did not hold in our simple form, but was
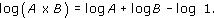
It was as a result of Briggs’ discussions with Napier that log 1 was redefined to be 0, thus simplifying this formula, and making the use of logarithms easier. Briggs, too, developed the calculation of logarithms of ordinary numbers, using the correlation log 10 = 1, log 100 = 2, log 1000 = 3, and so on.


