3 Napier’s approach to logarithms
Napier’s major and more lasting invention, that of logarithms, forms a very interesting case study in mathematical development. Within a century or so what started life as merely an aid to calculation, a set of ‘excellent briefe rules’, as Napier called them, came to occupy a central role within the body of theoretical mathematics.
The basic idea of what logarithms were to achieve is straightforward: to replace the wearisome task of multiplying two numbers by the simpler task of adding together two other numbers. To each number there was to be associated another, which Napier called at first an ‘artificial number’ and later a ‘logarithm’ (a term which he coined from Greek words meaning something like ‘ratio-number’), with the property that from the sum of two such logarithms the result of multiplying the two original numbers could be recovered.
In a sense this idea had been around for a long time. Since at least Greek times it had been known that multiplication of terms in a geometric progression could correspond to addition of terms in an arithmetic progression. For instance, consider
![]()
and notice that the product of 4 and 8 in the top line, viz 32, lies above the sum of 2 and 3 in the bottom line (5). (Here the top line is a geometric progression, because each term is twice its predecessor; there is a constant ratio between successive terms. The lower line is an arithmetic progression, because each term is one more than its predecessor; there is a constant difference between successive terms.) Precisely these two lines appear as parallel columns of numbers on an Old Babylonian tablet, though we do not know the scribe’s intention in writing them down.
A continuation of these progressions is the subject of a passage in Chuquet’s Triparty (1484). See the passage in Reading 1 below.
Reading 1: Nicolas Chuquet on exponents
A Boethius says in his first book and in the first chapter, the science of numbers is very great, and among the sciences of the quadrivium it is one in the pursuit of which every man ought to be diligent. And elsewhere he says that the science of numbers ought to be preferred as an acquisition before all others, because of its necessity and because great secrets and other mysteries which there are in the properties of numbers. All sciences partake of it, and it has need of none. […]
To understand the reason why denomination of number is added to denomination, and to have knowledge of the order of numbers which was mentioned in the first chapter, it is necessary in a continuous sequence, like 1, 2, 4, 8, 16, 32, etc, or 3, 9, 27 etc.
| Numbers | Denomination |
|---|---|
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
| 16 | 4 |
| 32 | 5 |
| 64 | 6 |
| 128 | 7 |
| 256 | 8 |
| 512 | 9 |
| 1 024 | 10 |
| 2 048 | 11 |
| 4 096 | 12 |
| 8 192 | 13 |
| 16 384 | 14 |
| 32 768 | 15 |
| 65 536 | 16 |
| 131 072 | 17 |
| 262 144 | 18 |
| 524 288 | 19 |
| 1 048 576 | 20 |
Now it is necessary to know that 1 represents and is in the place of numbers, whose denomination is 0.2 represents […] the first terms, whose denominations is 1.4 holds the place of the second terms, whose denomination is 2. And 8 is the place of the third terms, 16 holds the place of the fourth terms, 32 represents the fifth terms, and so for the others. Now whoever multiplies 1 by 1, it comes to 1, and because 1 multiplied by 1 does not change at all, neither does any other number when it is multiplied by 1 increase or diminish, and for this consideration, whoever multiplies a number by a number, it comes to a number, whose denomination is 0. And whoever adds 0 to 0 makes 0. Afterwards, whoever multiplies 2, which is the first number, by 1, which is a number, the multiplication comes to 2: then afterwards, whoever adds their denominations, which are 0 and 1, it makes 1; thus the multiplication comes to 2¹. And from this it comes that when multiplies numbers by first terms or vice versa, it comes to first terms. Also whoever multiplies 2¹ by 2¹, it comes to 4 which is a second number. Thus the multiplication amounts to 4². For 2 multiplied by 2 makes 4 and adding the denominations, that is 1 with 1, makes 2. And from this it comes that whoever multiplies first terms by first terms, it comes to second terms. Likewise whoever multiplies 2¹ by 4², it comes to 8³. For 2 multiplied by 4 and 1 added with 2 makes 8³. And thus whoever multiplies first terms by second terms, it comes to third terms. Also, whoever multiplies 4² by 4², it comes to 16 which is a fourth number, and for this reason whoever multiplies second terms by second terms, it comes to fourth terms. Likewise whoever multiplies 4 which is a second number by 8 which is a third number makes 32 which is a fifth number. And thus whoever multiplies second terms by third terms or vice versa, it comes to fifth terms. And third terms by fourth terms comes to 7th terms, and fourth terms by fourth terms, it comes to 8th terms, and so for the others. In this discussion there is manifest a secret which is in the proportional numbers. It is that whoever multiplies a proportional number by itself, it comes to the number of the double of its denomination, as, whoever multiplies 8 which is a third number by itself, it comes to 64 which is a sixth. And 16 which is a fourth number multiplied by itself should come to 256, which is an eighth. And whoever multiplies 128 which is the 7th proportional by 512 which is the 9th, it should come to 65 536 which is the 16th.
Chuquet made the same observation as above, that the product of 4 and 8 (‘whoever multiplies 4 which is a second number by 8 which is a third number’) gives 32, which is above the sum of 2 and 3 (‘makes 32 which is a fifth number’). Chuquet seems virtually to have said that a neat way of multiplying 4 and 8 is to add their associated numbers (‘denominations’) in the arithmetic series and see what the result corresponds to in the geometric series. (Of course, had he wanted to multiply 5 by 9, say, Chuquet would have been stuck.) And in The sand-reckoner, long before, Archimedes proved a similar result for any geometric progression.
So the idea that addition in an arithmetic series parallels multiplication in a geometric one was not completely unfamiliar. Nor, indeed, was the notion of reaching the result of a multiplication by means of an addition. For this was quite explicit in trigonometric formulae discovered early in the sixteenth century, such as:
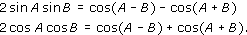
Thus if you wanted to multiply two sines, or two cosines, together – a very nasty calculation on endlessly fiddly numbers – you could reach the answer through the vastly simpler operation of subtracting or adding two other numbers. This method was much used by astronomers towards the end of the sixteenth century, particularly by the great Danish astronomer Tycho Brahe, who was visited by a young friend of Napier, John Craig, in 1590. So Napier was probably aware of these techniques at about the time he started serious work on his own idea, although conceptually it was entirely different.
Napier’s definition of logarithm is rather interesting. This course won’t pursue all its details here, but just enough to see its approach and character. Imagine two points, P and L, each moving along its own line.
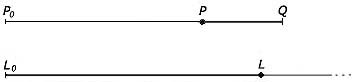
The line P0 Q is of fixed, finite length, but L’s line is endless. L travels along its line at constant speed, but P is slowing down. P and L start (from P0 and L0) with the same speed, but thereafter P’s speed drops proportionally to the distance it has still to go: at the half-way point between P0 and Q, P is travelling at half the speed they both started with; at the three-quarter point, it is travelling with a quarter of the speed; and so on. So P is never actually going to get to Q, any more than L will arrive at the end of its line, and at any instant the positions of P and L uniquely correspond. Then at any instant the distance L0L is, in Napier’s definition, the logarithm of the distance PQ. (That is, the numbers measuring those distances.) Thus the distance L has travelled at any instant is the logarithm of the distance P has yet to go.
How does this cohere with the ideas spoken of earlier? The point L moves in an arithmetic progression: there is a constant difference between the distance it moves in equal time intervals – that is what ‘constant speed’ means. The point P, however, is slowing down in a geometric progression: its motion was defined so that it was the ratio of successive distances that remained constant in equal time intervals.

Question 2
Compare what you have gleaned of Napier’s concept of logarithm with earlier ideas about progressions and trigonometrical formulae. What seems to you the most striking difference in overall approach? What problem do you see Napier’s work solving?
Discussion
The major difference is surely in his use of the concept of motion, of points moving along lines with speeds defined in various ways. Both exponents of Chuquet’s kind and trigonometrical formulae are quite ‘static’ objects by comparison – there is evidently a deep difference of mathematical style here.
What seems so clever about Napier’s approach is that he can cope with any number, in effect, not just the ones that happen to form part of some particular discrete geometrical progression. This is effected by his intuition springing from the continuous nature of the straight line and of motion.
