3.3.1 Try some yourself
Activity 14
If tomatoes cost 75 pence per kg, how much would 1.45 kg cost in pounds (£)?
Answer
The formula is
cost of tomatoes = (price per kilogram) × (number of kilograms).
The price per kilogram is 75 pence, and the number of kilograms is 1.45. So the formula gives
cost of tomatoes = (75 pence) × 1.45 = 108.75
Rounded to the nearest penny this is 109 pence, or £1.09.
Activity 15
If you travel in a car at a constant speed of 60 km per hour, how far would you have travelled after 1.5 hours, after 2 hours 40 minutes and after three and a half hours?
Answer
The formula is
distance travelled = (speed) × (time).
So, after 1.5 hours,
distance travelled = (60 km per hour) × (1.5 hours) = 90 km.
As 2 hours 40 minutes is 
hours, or 
hours, the formula gives
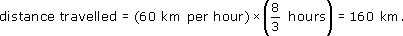
For three and a half hours (3.5 hours), the formula gives
distance travelled = (60 km per hour) × (3.5 hours) = 210 km.
Activity 16
3 Suppose you are selling a new lawn-edging strip and need to calculate the perimeters of lawns in order to quote prices to prospective customers.
The formula for the distance round the perimeter of a rectangular lawn is
perimeter = 2 × length + 2 × breadth.
Use this formula to find the perimeter of a lawn that is 10 m by 8 m.
Answer
The length of the lawn is 10 m and its breadth is 8 m. So, from the formula,
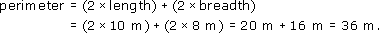
The perimeter of the lawn is 36 m.
Activity 17
Use the formulas for areas given below to find the areas of the shapes in square metres (m2).
Area square = (length)2; Area rectangle = length × breadth; Area triangle = 
base × height
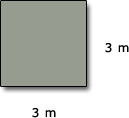
(a)
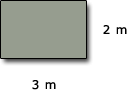
(b)
(c)
Answer
(a) Area square = (length)2 = (3 m)2 = 9 m2
(b) Area rectangle = length × breadth = 3 m × 2 m = 6 m2
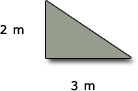
(c) Area triangle =
base × height = × 3 m × 2 m = × 6 m2 = 3 m2