3.3 Quantisation
The sample values measured during sampling must be quantised to produce a digital representation of the analogue signal. That is, each value is approximated to its nearest quantisation level. Quantisation levels are pre-determined levels, like the rungs of a ladder, between the lowest possible sample value and the highest. The closeness of the approximation between a sample value and its nearest quantisation level depends on the number of quantisation levels available. For example, using a thousand levels involves less approximation than using a hundred levels.
Each quantisation level is represented by a unique binary number. The number of levels is therefore related to the number of bits, n, used in the binary numbers that represent the quantisation levels. For example, using 3 bits provides eight (23) discrete levels represented by: 000, 001, 010, …, 111. Eight bits and twelve bits will quantise the signal into 256 (28) and 4096 (212) levels respectively. In general, an n-bit analogue-to-digital converter (ADC) provides 2n quantisation levels.
Activity 3.2 Self assessment
Compact disc audio uses 16-bit quantisation.
- a.How many quantisation levels are there?
- b.One quantisation level is designated as zero. Can there be equal numbers of levels for positive and negative values?
Answer
- a.For 16-bit quantisation, the numbers of quantisation levels is 216. This is 65 536.
- b.The number of quantisation levels in (a) is even, so there is no central value that can be designated as zero with equal numbers of positive and negative levels on either side. This is true whatever number of bits is used. For example, 3 bits gives 8 quantisation levels. If level 5 is taken as zero, there are four levels (1 to 4) on one side but three (6 to 8) on the other.
Quantisation inevitably introduces errors because the analogue signal can potentially take infinitely many values, whereas the number of quantisation levels is finite. You could compare this to a person standing on a staircase. The person’s height above the floor is restricted to the possibilities provided by the stairs. An object released over the side, however, passes through infinitely many heights as it falls to the floor.
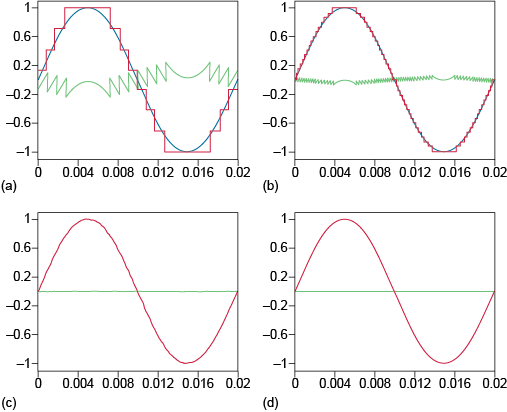
Figure 3.3 shows the effect of differing numbers of quantisation levels. A sine wave of amplitude 1 V is shown quantised into 8 levels (n = 3) in (a), 32 levels (n = 5) in (b), 256 levels (n = 8) in (c) and 65 536 levels (n = 16) in (d). The corresponding digital representations are shown in red and resemble steps outlining the sine wave. The difference between the original and digital signals is called quantisation noise (quantisation error) and is displayed in green. As n increases, the corresponding digital representation improves in fidelity because the quantisation noise (step size between adjacent discrete levels) is reduced. In Figures 3.3(c) and (d) the quantisation error is visually very small; nevertheless there will still be some quantisation noise present. This is why quantisation is lossy – in contrast to sampling, which is lossless provided the sampling theorem is upheld.
Quantisation is an example of lossy encoding because information is irretrievably lost when infinitely variable sample values are approximated by a set of quantisation levels. In audio work, 16 bits per sample is usual for the final files, giving 65 536 quantisation levels. The choice of 16 bits per sample is an example of perceptual, lossy encoding, in the sense that the choice of 16 bits per sample is based on properties of human hearing. More bits per sample is not considered to give any audible benefit and therefore results in unnecessarily large files. (Professional recording and editing often use more than 16 bits per sample, but this is not so much for higher fidelity as because some editing processes cause a deterioration of fidelity.) However, there is more to perceptual encoding than choosing a set of quantisation levels.
