Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Introduction to complex analysis
Introduction to complex analysis

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

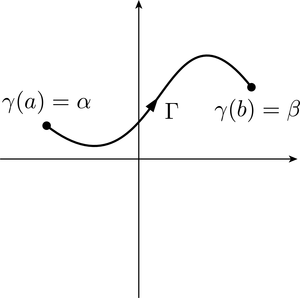
1.4 Introducing complex integration

We come now to the central theme of this course – integrating complex functions. Informed by the discussion in the introduction, we should expect that the integral of a continuous complex function f from one point alpha to another point beta in the complex plane may depend on the path that we choose to take from alpha to beta. So it is necessary to first choose a smooth path normal cap gamma colon gamma of t left parenthesis t element of left square bracket a comma b right square bracket right parenthesis such that gamma of a equals alpha and gamma of b equals beta (see Figure 14), and then we will define the integral of f along this smooth path, denoting the resulting quantity by

integral over normal cap gamma f of z d z full stop
Described image
Figure 14 A smooth path from alpha to beta
Show description|Hide description

This figure shows an unlabelled set of Cartesian axes concentrated in the upper-right and upper-left quadrants. There is an arbitrary point in the upper-left quadrant labelled gamma of a equals alpha and another arbitrary point in the upper-right quadrant labelled gamma of b equals beta. A path joins the two points and is marked with an arrow in a direction from point alpha to beta and labelled capital gamma. The curve starts at alpha then drops to a local minimum in the upper-left quadrant, it continues a local maximum in the upper-right quadrant then drops to point beta.

Figure 14 A smooth path from alpha to beta

There are two ways to achieve this goal.

One method is to imitate the approach of Section 1.2, as follows.

  • Choose a partition of the path normal cap gamma into subpaths

    cap p equals normal cap gamma sub one comma normal cap gamma sub two comma ellipsis comma normal cap gamma sub n comma

    determined by points alpha equals z sub zero, z sub one, …, z sub n equals beta, such as those illustrated in Figure 15.

    Described image
    Figure 15 (a) A partition of normal cap gamma (b) A partition of the line segment from zero to one plus i
    Show description|Hide description

    This figure has two parts: (a) and (b). Part (a) has a path which starts at the point z sub zero equals alpha and continues in an arbitrary manner from left to right to the final point z sub n equals beta. Along the path are four arrows in a left to right direction labelled capital gamma sub 1, capital gamma sub 2, capital gamma with an ellipsis underneath and finally capital gamma sub n. There are points marked on the path and labelled as follows. The point z sub 1 which is between the arrows capital gamma sub 1 and 2. The point z sub 2 which is between the arrows capital gamma sub 2 and capital gamma with an ellipsis underneath. The point z sub n minus 1 which is between the arrows capital gamma with an ellipsis underneath and capital gamma sub n. Part (b) shows an unlabelled set of Cartesian axes. There is a straight-line segment shown in the upper-right quadrant starting at the origin and this point is labelled z sub zero equals zero. The final point of the line segment is labelled z sub n equals 1 plus i. On the line segment are four arrows marked in a direction from the origin to the point 1 plus i labelled capital gamma sub 1, capital gamma sub 2, capital gamma with an ellipsis underneath and finally capital gamma sub n. There are points marked on the line segment and labelled as follows. The point z sub 1 which is between the arrows capital gamma sub 1 and 2. The point z sub 2 which is between the arrows capital gamma sub 2 and capital gamma with an ellipsis underneath. The point z sub n minus 1 which is between the arrows capital gamma with an ellipsis underneath and capital gamma sub n.

    Figure 15 (a) A partition of normal cap gamma (b) A partition of the line segment from zero to one plus i

  • Define a complex Riemann sum

    cap r of f comma cap p equals n ary summation over k equals one under n of f of z sub k times delta times z sub k comma

    where delta times z sub k equals z sub k minus z sub k minus one, for k equals one comma two comma ellipsis comma n, and define

    absolute value of cap p equals max of absolute value of delta times z sub one comma absolute value of delta times z sub two comma ellipsis comma absolute value of delta times z sub n full stop

  • Define the complex integral integral over normal cap gamma f of z d z to be

    lim over n right arrow normal infinity of cap r of f comma cap p sub n comma

    where left parenthesis cap p sub n right parenthesis is any sequence of partitions of normal cap gamma for which absolute value of cap p sub n right arrow zero as n right arrow normal infinity.

It can be shown (although it is quite hard to do so) that this limit exists when f is continuous, and that it is independent of the choice of partitions of normal cap gamma. Thus we have defined the integral of a continuous complex function. We can then develop the standard properties of integrals, such as the Additivity Rule and the Combination Rules, by imitating the discussion of the real Riemann integral.

The second, quicker method is to define a complex integral in terms of two real integrals. To do this, we use a parametrisation gamma colon left square bracket a comma b right square bracket long right arrow double-struck cap c of the smooth path normal cap gamma, where gamma of a equals alpha and gamma of b equals beta. Any set of parameter values

t sub zero comma t sub one comma ellipsis comma t sub n colon multirelation a equals t sub zero less than t sub one less than ellipsis less than t sub n equals b

yields a partition

cap p equals normal cap gamma sub one comma normal cap gamma sub two comma ellipsis comma normal cap gamma sub n

of normal cap gamma, where normal cap gamma sub k is the subpath of normal cap gamma that joins z sub k minus one equals gamma of t sub k minus one to z sub k equals gamma of t sub k, for k equals one comma two comma ellipsis comma n. We can then define the complex Riemann sum

cap r of f comma cap p equals n ary summation from k equals one to n over f of z sub k times delta times z sub k comma

where delta times z sub k equals z sub k minus z sub k minus one, for k equals one comma two comma ellipsis comma n; see Figure 16.

Described image
Figure 16 A partition of normal cap gamma induced by the parameter values t sub zero comma t sub one comma ellipsis comma t sub n
Show description|Hide description

This figure has two parts. On the left-hand side is a single unlabelled horizontal axis and on the right is an unlabelled set of Cartesian axes. There is a curved arrow linking the two labelled gamma. The left-hand axis is labelled with four points starting at the left with t sub zero equals a, then t sub 1, t sub k and finally t sub n equals b. A bold line segment joins the points a to b type. Underneath the line segment between the points t sub 1 and t sub k and t sub k and t sub n is an ellipsis. The right-hand set of axes is concentrated in the upper-right quadrant and has an arbitrary path marked with an arrow going from left to right and labelled capital gamma. The path starts at the point labelled z sub zero equals gamma of a and finishes at the point labelled z sub n equals gamma of b. The path is labelled as z sub k equals gamma of t sub k. The point z sub 1 equals gamma of t sub 1 is on the paths and labelled. There are two instances of an ellipsis shown under and along the path.

Figure 16 A partition of normal cap gamma induced by the parameter values t sub zero comma t sub one comma ellipsis comma t sub n

Notice that

equation sequence part 1 delta times z sub k equals part 2 z sub k minus z sub k minus one equals part 3 gamma of t sub k minus gamma of t sub k minus one full stop

Hence, if t sub k is close to t sub k minus one, then, to a good approximation,

multirelation gamma times super prime times left parenthesis t sub k right parenthesis almost equals gamma of t sub k minus gamma of t sub k minus one divided by t sub k minus t sub k minus one equals delta times z sub k divided by delta times t sub k comma

where delta times t sub k equals t sub k minus t sub k minus one, so

delta times z sub k almost equals gamma times super prime times left parenthesis t sub k right parenthesis times delta times t sub k full stop

Thus if max of delta times t sub one comma delta times t sub two comma ellipsis comma delta times t sub n is small, then, to a good approximation,

multirelation cap r of f comma cap p equals n ary summation from k equals one to n over f of z sub k times delta times z sub k almost equals n ary summation from k equals one to n over f of gamma of t sub k times gamma times super prime times left parenthesis t sub k right parenthesis times delta times t sub k full stop

The expression on the right has the form of a Riemann sum for the integral

integral over a under b f of gamma of t times gamma times super prime times left parenthesis t right parenthesis d t full stop
Equation label: (integral 1)

Here the integrand

t long right arrow from bar f of gamma of t times gamma times super prime times left parenthesis t right parenthesis times left parenthesis t element of left square bracket a comma b right square bracket right parenthesis

is a complex-valued function of a real variable. We have defined integrals of only real functions so far, but if we split f of gamma of t times gamma times super prime times left parenthesis t right parenthesis into its real and imaginary parts u of t plus i times v of t, then the integral (1) above can be written as

integral over a under b f of gamma of t times gamma times super prime times left parenthesis t right parenthesis d t equals integral over a under b u of t d t plus i times integral over a under b v of t d t comma

which is a combination of two real integrals. We then define the integral of f along normal cap gamma by the formula

integral over normal cap gamma f of z d z equals integral over a under b f of gamma of t times gamma times super prime times left parenthesis t right parenthesis d t full stop
Equation label: (formula 2)

It can be shown that both of these methods for defining the integral of a continuous complex function f along a smooth path normal cap gamma give the same value for

integral over normal cap gamma f of z d z full stop

In the next section we will develop properties of complex integrals, and there we will use the formula (2) above for the definition of the integral of a complex function f along a path normal cap gamma.

History of complex integration

The first significant steps in the development of real integration came in the seventeenth century with the work of a number of European mathematicians. Notable among this group was the French lawyer and mathematician Pierre de Fermat (1601–1665), who found areas under curves of the form y equals a times x super n, for n an integer (possibly negative), using partitions and arguments involving infinitesimals.

A major breakthrough was the discovery of calculus made independently by the English mathematician and scientist Isaac Newton (1642–1727) and the German philosopher and mathematician Gottfried Wilhelm Leibniz (1646–1716). They observed that differentiation and integration are inverse processes, a fact encapsulated in the Fundamental Theorem of Calculus.

Towards the end of the eighteenth century, mathematicians began to consider integrating complex functions.

Two pioneers in this endeavour were Leonhard Euler and Pierre-Simon Laplace. They were mainly concerned with manipulating complex integrals in order to evaluate difficult real integrals such as

integral over negative normal infinity under normal infinity sine of x divided by x d x equals pi and integral over negative normal infinity under normal infinity e super negative x squared d x equals Square root of pi full stop

However, it was through the work of Augustin-Louis Cauchy that complex integration began to assume the form that is now used in complex analysis. Cauchy’s first paper on complex integrals in 1814 treated complex integrals as purely algebraic objects; it was only much later that he came to properly appreciate their geometric significance.

By the mid to late nineteenth century, mathematicians began to consider how to expand the theory of integration to deal with functions that are not continuous. The first rigorous theory of integration to do this was put forward by Riemann in 1854. The Riemann integral was followed by a number of other formal definitions of integration, some equivalent to Riemann’s, and some more general, such as Lebesgue integration, named after the French mathematician Henri Lebesgue (1875–1941).