Skip to content
Skip to main content
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

About this free course

Become an OU student

Download this course

Share this free course

Course content Course content
Decision trees and dealing with uncertainty
Decision trees and dealing with uncertainty

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

4.2 A complex decision tree – deciding whether or not to launch a product early

From the last worked example, you should now have a good understanding of the basics of how decision trees work. In this next example in Activity 6 you will meet a more complex decision tree with more than just the initial decision node. In other words, more than one decision will be needed. Thus, as well as providing an initial decision (what to do now), the decision tree will also provide a strategy for future decisions depending on the outcomes of various chance events.

Activity 6 Example of a complex decision tree: considering early launch of a product

Timing: Allow approximately 45 minutes to complete this activity

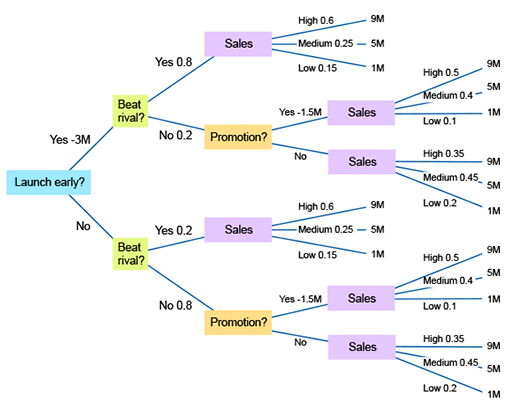
A company is planning on launching a new product. It was thinking of launching in June of next year but it believes that a rival is also considering launching a similar product around that time. The company is considering bringing the launch forward to the end of this year. This will cost an extra €3M to carry out and the company believes it will have a 0.8 probability of beating the rival to the market. If, however, they wait until June, the probability of beating the rival falls to 0.2.

To make the decision easier, the company assumes that sales will be either high, medium or low. If the company launches before its rival, the probability of high sales is 0.6 and the probability of medium sales is 0.25. If it launches after its rival, the probability of high sales falls to 0.35 and medium sales rises to 0.45. If the rival launches first, the company could undertake a sales promotion, costing €1.5M, but would change the probabilities of high sales to 0.5 and medium to 0.4.

The financial impacts are that high sales would be worth €9M, medium would be worth €5M and low, €1M.

Using a decision tree analysis, calculate what the company’s investment strategy should be. You can use pen and paper, an Excel spreadsheet, or record your calculations in the text box below.

Once you have arrived at a solution, watch Video 5 for the feedback of this activity.

To use this interactive functionality a free OU account is required. Sign in or register.
Interactive feature not available in single page view (see it in standard view).

Discussion

Now watch Video 5.

Download this video clip.Video player: Video 5
Copy this transcript to the clipboard
Print this transcript
Show transcript|Hide transcript

Transcript: Video 5 Solution for considering the early launch of a product

NARRATOR:
A company is planning on launching a new product. It was thinking of launching in June next year but believes that a rival is also considering launching a similar product. The company is considering bringing the launch forward to the end of this year. This will cost an extra 3 million euros to do, and the company believes it will have a 0.8 probability of beating the rival to the market. If, however, they wait until June, the probability of beating the rival falls to 0.2.
To make the decision easier, the company assumes that sales will be high, medium, or low. If the company launches before its rival, the probability of high sales is 0.6, and medium, 0.25. If it launches after, the probability of high sales falls to 0.35 and medium rises to 0.45. If the rival launches first, then the company could undertake a sales promotion costing 1.5 million euros but would change the probabilities of high sales to 0.5 and medium to 0.4.
The financial impacts are that high sales would be worth 9 million euros, medium, 5 million euros, and low, 1 million euros. So should the company launch this year or next? That's the big decision-- this or next. It'll cost an extra 3 million to launch this year. We'll note that for when we work out the expected value.
If we go up this branch, we need to take 3 million euros of the expected value. The company believes it will have a 0.8 probability of beating the rival to the market if it launches this year. So beat rival, yes or no, 0.8 here, therefore, this must be 0.2. If, however, the company waits until June next year, the probability of beating the rival falls to 0.2. So here we also put beat rival, yes or no branches, and it's 0.2 for yes and 0.8 for no.
So now we go to what type of sales we've got. We have three types-- high, medium, and low-- and the probabilities from this particular branch are 0.6, 0.25, and therefore, because they must all equal 1, 0.15. And then the values here are 9 million euros, 5 million euros, and 1 million euros.
If the company doesn't beat the rival to the market, then it has the opportunity to undertake a sales promotion. So this is a decision node. If it does the promotion, it will cost 1.5 million euros. And the sales will now have different probabilities; 0.5 for high, 0.4 for medium, and, therefore, 0.1 for low, but the end values will stay the same. If the company doesn't undertake a sales promotion, the probabilities are 0.35 for high, 0.45 for medium, and 0.2 for low. And again, the end values stay the same.
Now we move to launching the product next year. The sale nodes here are identical to the three at the top. They've all come after the "beating the rival" node. It's just the probabilities of getting there have changed. So this node here, with the one beside it, is the same as this node in terms of its expected value. It's just this one has 0.8 chance of it happening, whereas this one has a 0.2 chance. So whatever this expected value is, we put the same down here and the same with these.
Now let's work out the expected value at node one, which is 0.6 times 9 plus 0.25 times 5 plus 0.15 times 1, which is 6.8 million euros. We can also do the second node, 0.5 times 9 plus 0.4 times 5 plus 0.1 times 1 minus the 1.5 million to undertake the promotion. So we see that the expected value of undertaking a promotion is 5.1 million euros.
We'll put 6.8 on node one, and this will also be 6.8. Node two is 5.1, and so this is 5.1 as well. Now, we can work out the third sales node, where we didn't undertake a promotion. To work out this expected value, it's 0.35 times 9 plus 0.45 times 5 plus 0.2 times 1. There's no cost to deduct for this one, so the expected value is 5.6 million euros.
Node three's expected value can go here and also here. The company needs to decide whether to undertake a sales promotion. If they do, the expected value is 5.1 million euros. And if they don't, the expected value is 5.6 million euros. So based on these figures, the decision will be to not do a promotion.
Now we can go to node four. Remember, we're going right to left, and the expected value here is 0.8 times 6.8 plus 0.2 times 5.6, which is 6.56 million euros. And then node five is 0.2 times 6.8 plus 0.8 times 5.6. So node five is 5.84 million euros, and node four is 6.56 million euros.
Now, the only problem with node four is to get there, the company had to spend 3 million euros. So, in fact, the true cost here is the 6.56 minus the 3, which is 3.56 million euros. So the expected value of this route is 3.56 million euros, and the expected value of this route is 5.84 million euros.
So the company's strategy will be, first of all, not to bring the launch forward-- to launch the product next year. And if a rival beats the company to the market, it will not do the sales promotion.
End transcript: Video 5 Solution for considering the early launch of a product
Download
Video 5 Solution for considering the early launch of a product
Interactive feature not available in single page view (see it in standard view).

You may find it useful to work through the written solution below too. In this more complex decision tree you had to make some subsequent decisions based on the final outcomes of each branch. Thus you not only arrived at an initial decision (what action to take now) but also what actions to take at future points based on future chance events.

Written solution

You can also read the solution below.

The decision tree is shown in Figure 7.

Described image
Figure 7 Decision tree: a company deciding on when to launch a new product
Show description|Hide description

The first decision node asks ‘launch early?’

The top branch is for ‘yes’ which has a cost of 3m. Next on that branch is a chance node called ‘beat rival?’. This splits into two branches. The top brach is for ‘yes’ and has a 0.8 probability. This leads to a chance node called ‘sales’ which has three branches for high , medium and low. The respective probabilities are 0.6, 0.25 and 0.15. Finally there are the three respective final values starting with high sales 9 million, medium, 5 million And low 1 million.

Returning to the ‘beat rival?’ chance node the second branch is for ‘no’ and has a 0.2 probability. This leads to a decision node ‘promotion?’ which has two branches. The top branch is for ‘yes’ and costs -1.5 million and leads to a ‘sales’ chance node. This node has three branches for levels of sale, high , probability 0.5 and value 9 million, medium 0.4 probability and value 5 million and low, 0.1 probability 1 million.

Returning to the promotion node, the second branch is for ‘no’ and leads to a chance node ‘sales’ with three branches high, probability 0.35 value 9 million, medium 0.45 value 5 million and low 0.2 and 1 million.

Returning to the ‘launch early? Node the bottom branch is for no. Next on that branch is a chance node called ‘beat rival?’. This splits into two branches. The top branch is for ‘yes’ and has a 0.2 probability. This leads to a chance node called ‘sales’ which has three branches for high , medium and low. The respective probabilities are 0.6, 0.25 and 0.15. Finally there are the three respective final values starting with high sales 9 million, medium, 5 million And low 1 million. Returning to the ‘beat rival?’ chance node the second branch is for ‘no’ and has a 0.8 probability. This leads to a decision node ‘promotion?’ which has two branches. The top branch is for ‘yes’ and costs 1.5 million and leads to a ‘sales’ chance node. This node has three branches for levels of sale, high , probability 0.5 and value 9 million, medium 0.4 probability and value 5 million and low, 0.1 probability 1 million.

Returning to the promotion node, the second branch is for ‘no’ and leads to a chance node ‘sales’ with three branches high, probability 0.35 value 9 million, medium 0.45 value 5 million and low 0.2 and 1 million.

Figure 7 Decision tree: a company deciding on when to launch a new product

The calculations for each node are as shown in Table 9 (remember that you will need to work from right to left).

Expected sales

Table 9 Expected sales
Sales’ node number (from top to bottom of decision tree) Expected sales – calculation €M Expected sales – value €M
1 (0.6 × 9) + (0.25 × 5) + (0.15 × 1) 6.8
2 (0.5 × 9) + (0.4 × 5) + (0.1 × 1) 6.6
3 (0.35 × 9) + (0.45 × 5) + (0.2 × 1) 5.6
4 (0.6 × 9) + (0.25 × 5) + (0.15 × 1) 6.8
5 (0.5 × 9) + (0.4 × 5) + (0.1 × 1) 6.6
6 (0.35 × 9) + (0.45 × 5) + (0.2 × 1) 5.6

Expected sales after promotion

There are two promotion decision nodes, as summarised in Table 10.

Table 10 Expected sales after promotion
Promotion node number (from top to bottom of decision tree) Expected sales after promotion – calculation €M Expected sales after promotion – value €M
1 – Yes 6.6 – 1.5 5.1
1 – No 5.6 5.6
2 – Yes 6.6 – 1.5 5.1
2 – No 5.6 5.6

At both decision nodes, the expected value of sales is higher without the promotion than with it. The company will, therefore, never promote if launching after its rival. The higher figure of expected sales (€5.6m) is now carried forward.

Table 11 Expected sales at 'Beat rival?' chance node
‘Beat rival’ node number (from top to bottom of decision tree) Expected sales – calculation €M Expected sales – value €M
1 [(0.8 × 6.8) + (0.2 × 5.6)] − 3 3.56
2 (0.2 × 6.8) + (0.8 × 5.6) 5.84

You can see from Table 11 that the value of launching early is €3.56M, whereas the value of not launching early is €5.84M.

Thus, the decision is two-fold: the company should not launch early. If it then finds that it has not beaten its rival, it should not undertake a promotion.

In the next subsection you will consider another example of a complex decision tree, this time related to the launch of a new pharmaceutical drug.