1.1 Use of BODMAS and brackets
When several operations are combined, the order in which they are performed is important. For example, 12 + 21 x 3 might be interpreted in two different ways:
Activity 1
(a) add 12 to 21 and then multiply the result by 3
Answer
The first way gives a result of 99.
(b) multiply 21 by 3 and then add the result to 12
Answer
and the second a result of 75.
Discussion
We need some way of ensuring that only one possible interpretation can be placed upon the formula presented. For this we use BODMAS. BODMAS give us the correct sequence of operations to follow so that we always get the right answer:
- (B)rackets
- (O)rder
- (D)ivision
- (M)ultiplication
- (A)ddition
- (S)ubtraction
According to BODMAS, multiplication should always be done before addition, therefore 75 is actually the correct answer according to BODMAS.
(‘Order’ may be an unfamiliar term to you in this context but it is merely an alternative for the more common term, ‘power’ which means a number is multiplied by itself one or more times. The ‘power’ of one means that a number is multiplied by itself once, i.e., 2 x 1, 3 x 1, etc., the ‘power’ of two means that a number is multiplied by itself twice, i.e., 2 x 2, 3 x 3, etc. In mathematics, however, instead of writing 3 x 3 we write 3 2 and express this as three to the ‘power’ or ‘order’ of 2.)
Brackets are the first term used in BODMAS and should always be used to avoid any possibility of ambiguity or misunderstanding. A better way of writing 12 + 21 x 3 is thus 12 + (21 x 3). This makes it clear which operation should be done first.
12 + (21 x 3) is thus done on the calculator by keying in 21 x 3 first in the sequence:
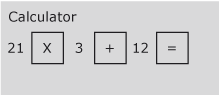
Activity 2
Complete the following calculations.:
Part (a)
(a) (13 x 3) + 17
Answer
(a) 56
Part (b)
(b) (15 / 5) – 2
Answer
(b) 1
Part (c)
(c) (12 x 3) /2
Answer
(c) 18
Part (d)
(d) 17 – (3 x (2 + 3))
Answer
(d) 2 (Hint: did you enter the expression in the inner brackets i.e. (2 +3) first?)
Part (e)
(e) ((13 + 2) / 3) –4
Answer
(e) 1
Part (f)
(f) 13 x (3 + 17)
Answer
(f) 260
