3 Designing alternative programmes and curricula
Assuming that both the content of mathematics and the processes need to be included in programmes and curricula, the problem becomes one of how a suitable curriculum can be structured. One possibility is to construct a very specific curriculum with clearly defined objectives for both content and processes separately, and possibly with suggested learning activities. However, content and process are two complementary ways of viewing the subject.
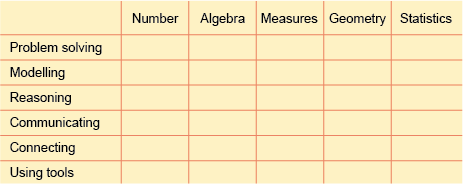
An alternative is to see the curriculum in a two-dimensional array with content areas drawn against processes; to use a weaving metaphor, one can be thought of as the weft and the other the warp. The five major content areas (number, algebra, measurement, geometry, statistics) and the six key processes (problem solving, mathematical modelling, reasoning, communicating, making connections, using tools) would therefore form the thirty combinations indicated in the matrix in Figure 1.
Activity 8 Using a content/process matrix
What is your initial response to the matrix in Figure 1?
Think of a mathematics lesson. What was the content of that lesson? Can you identify any mathematical processes that the learners used during the lesson (you will need to look again at the Appendix: processes uncovered to remind yourself of the detail of these processes)?
Comment
Some teachers (and learners) find it difficult to identify mathematical processes, particularly modelling and connecting. This course is designed to help you become aware of a range of mathematical processes and to consider how they can be used to encourage learning.
It may help you to look back at the Appendix when you are working on later activities in this course. Try to be aware of the mathematical processes you are using as well as the more obvious areas of mathematical content involved.
Activity 9 Reading
Read the short story Appendix: Paul Bunyan versus the conveyor belt (Upson, 1964). While you are reading, note down your reactions to it.
Comment
The article shows a clear link between mathematics and the procedure of solving an everyday problem. But it is this link between school mathematics and everyday life that many learners find problematic. Articles like this one can be a useful catalyst for motivating learners and encouraging classroom discussion and investigation.
When you were reading the article you might have also been aware of how you could use it with your learners. If you felt it inappropriate to read the article in full to your learners you could summarise the story. Using articles and stories in this way can provide useful examples of the links between everyday life and mathematics.
Activity 10 Process
Look back at the article and work out what processes Bunyan used when working on the conveyor belt problem. List them in your notebook; you will need these later.
So far you have read an article – that is, you have done something. You have also recorded some notes about what you read. You may also have talked to yourself or with a colleague in order to understand the article more clearly. As you will see in the final section of this course, these three elements form a useful framework for helping you to think about learner learning. It will be referred to as the DTR triad.