4  Do–talk–record triad

The DTR triad is a description of what is likely to take place in collaborative mathematics classrooms. It is concerned with observable events, and with the learner rather than the teacher, though many teaching insights flow from it. Although the order of the triad suggests that it should be followed in a particular sequence, this is not necessarily the case. Sometimes talking comes before doing or recording before talking. It also takes time for a learner to move from doing and talking to recording and back to doing again. At each stage the learner needs time to think and reflect on their work and results.

In a classroom where DTR is in use, you are likely to see learners who are prepared:

• to think for themselves
• not to be afraid to communicate their thinking for fear it may be wrong
• to accept that wrong answers can be helpful
• to listen to their peers for comments in their own words
• to question their peers’ ideas asking for justification, examples, or proof.

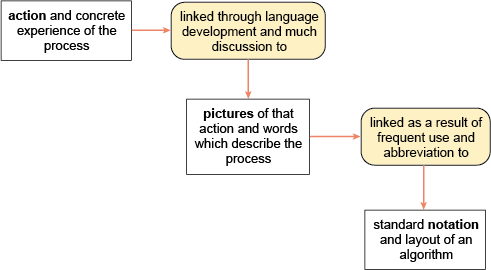
In the classroom, teaching with an emphasis on DTR would look like the framework in Figure 3.

Figure 3 Do–talk–record framework

Show description|Hide description

The do–talk–record framework is a series of five boxes with text in. The first box text is ‘action and concrete experience of the process’, an arrow leads from this box to the second box. The second box text is ‘linked through language development and much discussion to’, an arrow leads from this box to the third box. The third box text is ‘pictures of that action and words which describe the process’, an arrow leads from this box to the fourth box. The fourth box text is ‘linked as a result of frequent use and abbreviation to’, an arrow leads from this box to the fifth, and final, box. The fifth box text is ‘standard notation and layout of an algorithm’.

Figure 3 Do–talk–record framework

This framework links with ideas of going from the concrete to the abstract, and with notions of the importance of practical, kinaesthetic, or enactive experience on which to build understanding. It emphasises too the importance of language in learning, both the learners’ own language and the language of mathematics.

The ideas implicit in this DTR framework are set out in Table 2.

In many mathematics classrooms, it is common for doing and recording to take priority over talking. But it is the act of verbalising a problem that can often be of most help. Teachers can help with this verbalisation by the use of prompts such as the following:

• Explain the question to me.
• What do you know?
• What are you trying to find out?
• What have you done so far?

Often it is the act of verbalisation and the hearing of the words that provides a key to moving forward. It may be the case that hearing the words in your head is not enough, in which case say them out loud, even if you are not talking to anyone.

You have worked on the Möbius band problems yourself so now it is time to work with learners. The way you approached the activity may be different from that of your learners. Remember to note down any differences or similarities.

Before you proceed further think about the activity you have just completed, the mathematics involved, and the strategies you used. Were you surprised by some of the results? Jot down any further reflections in your notebook.