2.8 Stomata
The following video explains what stomata are and their function in gas exchange between the inside of a leaf and the air. To appreciate the size, abundance and rate of movement of the guard cells that form stomata, some measurements and calculations are needed. Using information from the video and some additional details you can calculate the number of stomata on a leaf and a whole tree! You should also consider why they might not move more quickly. There are quite a few calculations in this section, but you will be stepped through them.
While watching the video, record the following information to use in the questions that follow:
- the length of a guard cell to the nearest micrometre (μm)
- the density of stomata (per square millimetre) on the upper surface of an oak leaf
- how long it takes stomata to open or close, to the nearest 5 minutes. (You will need to use the clock in the top left-hand corner of the video to estimate this.)

Question 1
What is the length of a guard cell, to the nearest micrometre?
Question 2
The density of stomata is the number of stomata in a given area. In the video, stomatal density is stated as the number of stomata per square millimetre (stomata per mm2, or stomata mm−2). If the average size of an oak leaf is 15 cm2, you can use the density of stomata to work out roughly how many stomata are on the top side of a leaf. Let’s go through the calculations step by step. You may find Figure 7 will help you to visualise the scales.
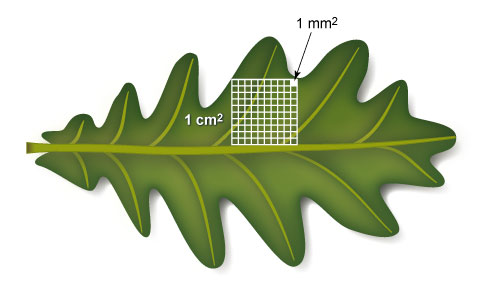
Question 3
First, how many square millimetres are there in a square cm?
Question 4
Discussion
Note the way that the units were derived for the final answer. In multiplying ‘stomata mm−2’ by ‘mm2 cm−2’ the ‘mm’ terms cancelled each other out, leaving just ‘stomata cm−2’.
Question 5
Finally, use your answer to Question 4 to work out how many stomata there are on the upper surface of a leaf which has an area of 15 cm2. Provide your answer using standard scientific notation.
Question 6
The video indicated that there is a higher density of stomata on the lower surface of the leaf (500 stomata mm−2). Using this value and the answer to Question 5, work out the total number of stomata on both sides of the leaf.
Discussion
Another way to work out the answer to this question is to consider the ratio of stomatal density between the upper and lower side of the leaf. Using the stomata densities on either side of the leaf – 500 mm−2 on the lower side and 100 mm−2 on the upper side – it is possible to calculate that there are
times as many stomata on the lower side.
Using this ratio, if there are 1.5 × 105 stomata on the upper surface there must be 7.5 × 105 on the lower side. Adding the two numbers together gives the total number of stomata on the leaf as 9.0 × 105.
Question 7
A large oak might have 400 000 leaves in a single year. How many stomata would there be on a tree with this many leaves?
Discussion
Clearly these are estimates, as the actual number of stomata on every leaf, or even exactly how many leaves are on the tree haven’t been counted. However, these values are based on numbers published in scientific reports for Quercus robur and should provide a reasonable estimate. Next time you walk past a large tree, take a minute to think about how many stomata their might be on the whole tree… and then think about how many stomata there might be in a forest!
Researchers use high precision equipment, such as leaf chambers and infrared gas analysers to measure the amount of CO2 taken up by a leaf over time (Figure 8). You can use the information from such measurements together with your earlier calculations to estimate the number of CO2 molecules taken up by stomata.

Question 8
Experiments have shown that an oak leaf in sunlight can take up CO2 at a net rate of 4.4 × 10−9 grams per cm2 of leaf per second (or 4.4 × 10−9 g CO2 cm−2 s−1). Calculate the mass of carbon dioxide taken up by one stomata in one second by dividing this value by the number of stomates in a cm2 of leaf.
Discussion
You can turn this mass of CO2 into a number of molecules of CO2.
It turns out that 44 g of CO2 contain 6.023 × 1023 molecules (this is called Avogadro’s number).
So if there are 6.023 × 1023 molecules in 44 g of CO2 there must be
To calculate the number of molecules of CO2 taken in by each stomata per second you now need to multiply the mass of CO2 per stomata per second by the number of molecules of CO2 per gram of CO2.
This gives a value of 1.0 × 109 molecules CO2 stomata−1 s−1. That is 1 billion molecules of CO2 per stomata per second!
Each of the stomata will open and close during the day to regulate CO2 uptake and water loss. Now it is time to consider the time it takes stomata to open and close.
Question 9
How long does it take a stomata in the animation to open and close (to the nearest 5 minutes)?
Question 10
In oaks, light stimulates stomata to open and lack of light stimulates closure. Why might stomatal closure take some minutes rather than being instantaneous? Suggest possible reasons. Note: this question is to encourage you to consider possibilities rather than necessarily knowing the ‘right’ answer. (Your answer should be between 50 and 100 words.)
Answer
Light levels can change very quickly, as a leaf can be shaded by others intermittently in windy conditions or as clouds roll by. The plant uses energy to open and close stomata, which could be wasted if the stomata were to respond too quickly to environmental conditions. However, if the weather clouds over for a long time, or the leaf moves into long-term shade and low light levels prohibit photosynthesis, stomata need to close to reduce water loss.
Summary
In this section you learned that microscopic guard cells form stomata or pores, which allow billions of molecules of CO2 to be exchanged between the leaf and the atmosphere every second. The stomata open and close to regulate the movement of gases. Through a series of calculations, you were able to consider just how many stomata there are on a leaf and a whole tree. There were some really massive numbers there!
Although this section focuses on the scale of cells (micrometres) your calculations showed how process at this scale affect bigger (leaves and trees) and smaller (molecules) size scales.
Next: Now look at the components of a leaf at even smaller scales by examining a chloroplast within a stomatal cell, which you can do with the ‘Next >’ button, or you can return to the size–time explorer [Tip: hold Ctrl and click a link to open it in a new tab. (Hide tip)] to choose a level for yourself.
