Find out more about The Open University's Mathematics courses.

Periodic tiles

Imagine tiling your bathroom with square tiles. Square tiles will fit together perfectly to cover the whole wall. In fact, if you had infinitely many square tiles, you could use them to cover an infinite flat surface.

The downside is that the pattern is quite boring. In fact, if you take a copy of the pattern, and slide it to the right, all the tiles will line up and you have the exact same pattern as before. In other words, the pattern repeats.

We could also tile the infinite surface using triangles or hexagons and get the same result. On the other hand, some shapes such as pentagons cannot tile the surface, because pentagons will always leave gaps.

We could also tile an infinite surface using more than one shape. Here is an example that uses two shapes.

These two shapes will tile an infinite surface forever. But, again, if we shift the tiles to the right, we can see that the pattern repeats.

Tilings like this have a long history and have been used since ancient times as decorative art – from Islamic art to Roman mosaics. Tilings can be made from one or more shapes, and the tiles can be made from regular or irregular polygons. If the pattern repeats, the tiling is call periodic.

But is it possible to have a set of tiles, that can cover the infinite surface such that the pattern never repeats? And if so, what would these tiles look like?

Aperiodic tiles

In 1961, Hao Wang, a Chinese mathematician and philosopher, proposed that any finite set of tiles that can cover the infinite surface must have at least one periodic tiling. So, even if the tiles have many possible patterns, there would be at least one pattern that would be periodic.

However, this was shown not to be true, when Wang’s student, Robert Berger, found a set of 20,426 tiles that could be used to cover the infinite surface, without ever being periodic.

Such a set of tiles is called aperiodic because they can never form a periodic pattern. 

Aperiodic tilings, like the kind found by Wang and Berger, are used in computer graphics to give surfaces texture without any noticeable patterns. However, a set of over twenty-thousand tiles is quite unwieldly, even for a computer. 

Robert Berger himself was able to reduce the number of tiles, from 20,426, down to just 104. But, can we reduce this number even further?

In fact, by the late 1970s, this number was reduced to just two.

Penrose tiles

Below is a non-repeating pattern made from two tiles. These tiles cover the infinite surface but will never create a repeating pattern - they are aperiodic tiles.

This set of two tiles was discovered in 1976 by the English mathematical physicist Roger Penrose.

Penrose based his set of tiles on Pentagons, which are difficult to tile, even with other shapes. Penrose incorporated the same disruptive properties of the pentagon to create two tiles that form an aperiodic set.

This set of Penrose tiles uses a thin rhombus and a fat rhombus. Ordinarily, rhombus-shaped tiles can be used to tile the infinite surface periodically, so Penrose modified the edges to eliminate repeating patterns, and so create aperiodicity.

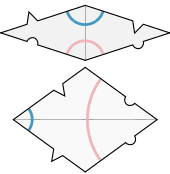
Another famous set of Penrose tiles are the kite and dart. The idea here is to match the lines, so although it’s tempting, we cannot use the kite and dart to make a rhombus. This is similar to modifying the edges to ensure aperiodicity.

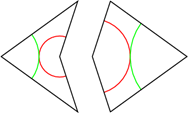
With these rules, you can make non-repeating patterns like this:

Parts of a Penrose tiling have the same symmetry as a pentagon (five-fold rotational symmetry and five mirror lines of reflective symmetry). This only true for finite areas (not the whole infinite tiling), but the finite areas can be quite large.

Since their discovery, Penrose tiles have been used as art and decoration in architecture, including the floor of the department of mathematics at Oxford University and at San Francisco’s transit centre. 

Aperiodic tiles are also used in the study of material with naturally aperiodic structure, known as quasicrystals. Quasicrystals have unique material properties and applications are being investigated.

But since the discovery of Penrose’s two tile sets, mathematicians have wondered, is it possible to create an aperiodic set of tiles consisting of just one tile – an aperiodic monotile! Well, that discovery took another 45 years.

The Einstein and the spectre

The problem to cover the infinite flat surface, aperiodically, with just one tile, became known as the einstein problem. Not to be confused with Albert Einstein, but a play on “ein Stein”, the German for “one stone”.

Although many had attempted to find the aperiodic monotile before, no one succeeded until David Smith in 2023.

The image above is of the hat, aligned to its underlying grid.

Smith’s tile was based on the hexagon, which allows it to cover the infinite surface. But Smith also noticed that the patterns it created seemed to be aperiodic. 

Nicknamed “the hat”, this tile was proved to be aperiodic in a paper by Smith, Myers, Kaplan and Goodman-Strauss. https://arxiv.org/abs/2303.10798

The hat tiles the infinite surface using just rotations and reflections of itself. In fact, Smith and the others found a whole family of tiles, like the hat, that could tile the surface in the same way.

The image above is of hat tiles - the surface with rotations and reflections (in dark red).

One member of this family had the extra special property. It could tile the infinite surface aperiodically, and it could do so without using reflections. This extra special tile is the spectre - because it doesn’t have a reflection.

The image above is of the spectre tiling without reflections.

The discovery of the spectre tile finally solved the 60-year-old problem of the aperiodic monotile, and it may lead to some exciting applications.

Applications

Mechanical metamaterials are man-made materials with internal honeycomb-like structures that can make materials stronger yet lighter, and better at handling heat and absorbing energy. 

Thanks to new 3D printing technologies, researchers at the Open University, and elsewhere, can now investigate the properties of more complex honeycomb designs, including designs based on aperiodic tilings.

Most excitingly, honeycomb material based on the hat tile show zero sideways stretching when squeezed - a rare and useful trait shared with natural materials like cork. 

The gif above shows squeezing square and hat honeycombs.

This could lead to new materials for industries where stability under pressure is critical, such as in medical devices (like stents), aerospace engineering (like shape-shifting wings), and packaging (like safe bottle stoppers). 

Or, we can be like the Romans, and use the aperiodic monotile to create the best mathematical bathroom.