11.2 Fformiwlâu ar waith
Byddwch eisoes wedi dod ar draws fformiwlâu yn eich bywyd pob dydd, ac wedi’u defnyddio. Er enghraifft, os ydych yn ceisio gweithio allan cost carped newydd byddwch wedi defnyddio’r fformiwla:
arwynebedd = hyd × lled
i gyfrifo faint o garped byddai arnoch ei angen.
Yn aml caiff rhannu mewn fformiwla ei ddangos fel un rhif dros un arall, er enghraifft:
dangosir 6 ÷ 3 fel
Dewch inni edrych ar rannu mewn fformiwla:
Mae gyrrwr lori’n teithio 120 o filltiroedd mewn 3 awr. Beth oedd y cyflymder cyfartalog yn ystod y daith?
Noder Gan ei bod yn annhebygol y byddai’r gyrrwr wedi teithio ar gyflymder cyson am 120 o filltiroedd, rydym yn cyfrifo’r cyflymder cyfartalog gan y bydd hwn yn rhoi’r cyflymder cyflawn nodweddiadol.
cyflymder =
cyflymder = 40 milltir yr awr
Weithiau rydym yn defnyddio llythrennau i gynrychioli’r elfennau gwahanol a ddefnyddir mewn fformiwla, e.e. gellid dangos y fformiwla uchod fel:
c =
lle:
‘c’ = cyflymder mewn mya
‘p’ = pellter mewn milltiroedd
‘a’ = amser mewn oriau
Os ydych yn ceisio gweithio allan yr amser i goginio cyw iâr ffres, efallai eich bod wedi defnyddio’r fformiwla:
Amser (munudau) = 15 + × 25 lle ‘p’ yw pwysau’r cyw iâr mewn gramau.
Er enghraifft, os oeddech eisiau coginio cyw iâr sy’n pwyso 2500 g, byddech yn gwneud:
Amser (munudau) = 15 + × 25
Gan gofio defnyddio CORLAT, byddech yn cael:
Amser (munudau) = 15 + 5 × 25
= 15 + 125
= 140 o funudau
Dewch inni edrych ar enghraifft arall wedi’i chyfrifo cyn ichi roi cynnig ar rai ar eich pen eich hun.
Enghraifft: Fformiwla bil nwy
Mae perchennog gwesty’n cael bil nwy. Cafodd ei gyfrifo gan ddefnyddio’r fformiwla ganlynol:
Cost nwy (£) =
Noder: Ystyr 8d yw 8 × d.
Lle mae d = nifer y diwrnodau ac u = nifer yr unedau a ddefnyddiwyd. Os yw’r perchennog wedi defnyddio 3500 o unedau o nwy mewn 90 o ddiwrnodau, faint yw’r bil?
Yn yr enghraifft hon, d = 90 ac u = 3500 felly rydych chi’n gwneud:
Cost nwy (£) =
=
=
= £42.20
Gweithgaredd 31: Defnyddio fformiwlâu
Caiff defnydd tanwydd yn Ewrop ei gyfrifo mewn litrau y 100 cilometr. Fformiwla ar gyfer trosi yn fras o filltiroedd y galwyn i litrau y 100 cilometr yw:
L =
lle L = nifer y litrau y 100 cilometr a M = nifer y milltiroedd y galwyn.
Mae car yn teithio 40 milltir y galwyn. Beth yw hwn mewn litrau y cilometr?
Ateb
- L = ac yn yr achos hwn M = 40
- L =
- L = 7 litr y 100 cilometr
Gan ddefnyddio’r fformiwla Ll = lle:
Ll = llog
P = prifswm y benthyciad
C = cyfradd llog
A = amser mewn blynyddoedd
cyfrifwch faint o log sy’n ddyledus ar fenthyciad o £5000 a gymerwyd dros 3 blynedd ar gyfradd llog o 5.5%.
Ateb
Ll =
Yn yr achos hwn, P = £5000, C = 5.5% ac A = 3 blynedd.
Ll =
Ll =
Ll = 825
Felly’r llog a dalwyd yw £825.
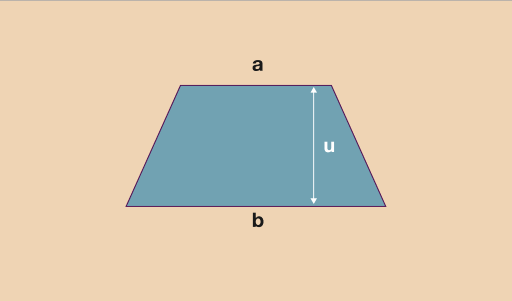
Gellir cyfrifo arwynebedd trapesiwm trwy ddefnyddio’r fformiwla:
A =
Canfyddwch arwynebedd trapesiymau lle:
- i.a = 5 cm, b = 9 cm ac u = 7 cm
- ii.a = 35 mm, b = 40 mm ac u = 10 cm
Ateb
A =
i.A =
A =
A =
A = 49 cm2
ii.Yn y cwestiwn hwn, rhaid ichi drosi’r unedau fel eu bod i gyd yr un fath. Yr unedau a ddewiswch fydd yr unedau y rhoddir eich ateb ynddyn nhw e.e. os ydych yn trosi i mm bydd eich ateb mewn mm2, ond os ydych yn trosi i cm, bydd eich ateb mewn cm2.
A =
Dull 1 – trosi i mm
Troswch y mesuriad h i mm:
10 × 10 = 100 mm
A =
A =
A =
A = 3750 mm2
Dull 2 – trosi i cm
Troswch fesuriadau a a b i cm:
a = 35 ÷ 10 = 3.5 cm
b = 40 ÷ 10 = 4 cm
A =
A =
A =
A = 37.5 cm2
Noder mae’n syniad da dangos holl gamau’r cyfrifiad i’ch helpu i gadw golwg ar eich gwaith cyfrifo.
Mae cwmni’n defnyddio’r fformiwla ganlynol i weithio allan cyfanswm y gost i gwsmer am logi castell gwynt:
T = hc + (0.45d) + 15
lle:
T = cyfanswm
h = nifer y diwrnodau a logwyd
c = cost y castell fesul diwrnod
d = pellter cludo mewn milltiroedd
Mae Stuart yn byw 12 milltir i ffwrdd, a hoffai logi Castell y Gofod am 2 ddiwrnod. Faint fydd yn costio?
Ateb
T = hc + (0.45d) + 15
Yn yr achos hwn, h = 2, c = £42, a d = 12, felly:
T = 2 × 42 + (0.45 × 12) + 15
T = 84 + 5.4 + 15
T = 104.4
Cyfanswm cost llogi castell gwynt yw £104.40.
Nawr eich bod wedi dysgu’r holl sgiliau sy’n berthnasol i adran rhifau’r cwrs hwn, dim ond un peth arall mae angen ichi fod yn gallu ei wneud cyn y byddwch yn barod i gwblhau’r cwis diwedd sesiwn ar gyfer rhifau.
Erbyn hyn rydych yn hyfedr wrth wneud llawer o gyfrifiadau gwahanol gan gynnwys gweithio allan ffracsiynau a chanrannau rhifau, defnyddio cymarebau mewn cyd-destunau gwahanol a defnyddio fformiwlâu.
Mae’n wych eich bod yn gallu gwneud yr holl bethau hyn, ond sut ydych chi’n gwirio a yw’r ateb yn gywir? Un ffordd o wirio yw brasamcanu ateb i’r cyfrifiad (fel y gwnaethoch yn Adran 3.2). Ffordd arall i wirio ateb yw defnyddio’r gweithrediad gwrthdro (dirgroes).
Crynodeb
Yn yr adran hon, rydych wedi:
- dysgu am, ac ymarfer defnyddio CORLAT – y drefn mae’n rhaid gwneud gweithrediadau ynddi
- gweld enghreifftiau o fformiwlâu a ddefnyddir mewn bywyd pob dydd ac wedi ymarfer defnyddio fformiwlâu i ddatrys problem.