3 A flat map of a spherical world
A geographical map is a two-dimensional representation of the actual physical topography of a geographical region, and whilst almost everyone is familiar with, for example, a road map, mapping is a complex subject. The making of maps is called cartography and fundamentally it is about the relationship between data (the information you wish to display and convey) and space. This is both the geographic space being represented and the space available on a sheet of paper or display screen. The data are represented by points (to show location) and lines (to show connections or borders), by symbols (to convey features), and finally by names and colour and/or shading (to represent areas). Of course, the names of places, like London, or contour lines representing height, don’t physically appear on the ground where they are shown on maps!
One of the challenges facing cartographers as they try to express both data and space at the largest scales (i.e. the whole Earth or large sections of it) is the classic problem of representing features on the curved surface of a spherical Earth (or globe, see Figure 4) on a plane (or flat) surface.
Activity 2 Shapes on a peeled orange
Take an orange and draw the outline of two shapes on its peel with a felt pen. On one side draw a circle and on the other a square, making sure your shapes cover at least a third of the surface of the orange. Now peel the orange, trying to leave the skin in one piece. Take your peel, and put some cuts in it at the edges with a knife or scissors so that it will lie completely flat on a table.
Can you still see your shapes with exactly the same outline as when you drew them?
Answer
You were asked to draw two large shapes so that you can see the distortion. Depending on where you put your cuts it is unlikely that your shapes will be exactly as you originally drew them. In the jump from three dimensions to two dimensions the shape has become distorted. The way this distortion is avoided is by using a map projection.
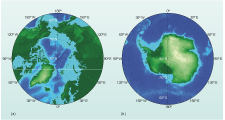
In your answer to Activity 2, whether you could see your shapes in the same way you drew them depends on where you made the cuts. But it is possible to make a flat drawing of the surface of the orange with your shapes on to show them as you actually drew them. This is called a map projection. All projections involve some sort of compromise because it is just not possible to keep everything completely accurate when shifting from three dimensions to two. An example of a projection of map data is shown in Figure 6a, which is the Earth in what is called the Lambert equal-area azimuthal projection. It is round like Figure 4 and you should be able to recognise some of the land shapes in this map.
Is it possible for you to hold an orange or apple in such way that you can see both poles as shown in Figure 6a?
No! You can only see the top or the bottom at one time.
Figure 6a is clearly distorted so that both poles are visible.
What are the most distorted countries shown in Figure 6a?
Australia is completely unrecognisable along with the Pacific coast of Russia and North America.
In Figure 6a, the amount of distortion changes with distance from the centre of the map at 0° N 0° E. To demonstrate this, there are a number of circles overlain on the picture. Each one of the circles encloses an equal surface area of the Earth. If you think back to your orange, imagine covering it with regularly spaced round stickers about 1 cm across. Each sticker would cover the same surface area of the orange. But in the projection in Figure 6a the size of the circles is varying – they are larger the further away they are from the centre of the map.
If the circles appear larger but are actually the same size, what is happening to the surface area that they cover?
The surface area is being distorted on the map so that it appears larger.
If there was no distortion in the projection, then all of the circles would be the same size all over the map.
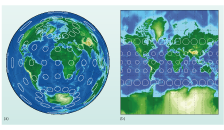
A commonly used map projection is the Mercator projection (Figure 6b) and on it the lines of longitude and latitude cross at right angles. This picture also has the same circles as Figure 6a which cover an equal area.
How do the circles change size relative to the Equator in the Mercator projection?
The circles are equal in size along lines of latitude near the Equator but increase in size with distance from the Equator.
Clearly the Mercator projection is distorting land away from the 0° latitude line.
Based on the size of the circles, how are Greenland and Antarctica distorted by the Mercator projection relative to their actual size?
Because the circles are larger towards the poles, the Mercator projection shows Greenland and Antarctica as larger than they should be. As there is no single point for a pole, Antarctica is virtually unrecognisable.
The Mercator projection is often used for maps with a small range of latitudes so there will not be very much distortion. When there is a large range of latitude like in Figure 6b, it is not easy to determine the relative sizes of different regions. There are many different projections and it is important to keep in mind that all of them distort geographic data to a certain extent. The key is to choose a projection that distorts your geographic region of interest the least. This course is focused on the polar regions and for this reason you will frequently encounter what is called the stereographic projection (Figure 7a, b), which is equivalent to being above the North and South Poles and looking downwards. The stereographic projection is very good for showing the high latitudes as there is only significant distortion at large distances from the poles.
Looking at the stereographic projection starting at the pole and working outwards, the lines of equal latitude are dotted and increasing in size (as shown in Figure 5). In Figure 7, the first dotted circle is at 75° north (or south) and the second 60° north (or south). Lines of equal longitude are just like hours on a clock, and are described in Figure 5.