8.2 P-value

We can also find the p-value for t-test using Excel functions. For t-test, the Excel function is more complex than z-test. We have three different functions.

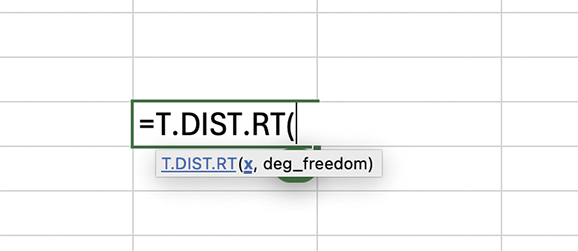
Upper Tailed (One-Tailed) t-Test:

Formula: =T.DIST.RT(x, deg_freedom)

Figure 26 T.DIST.RT function.

Show description|Hide description

The image shows the Excel function T.DIST.RT, which calculates the right-tailed probability of the Student’s t-distribution. It requires two inputs: x, the value to evaluate, and deg_freedom, the degrees of freedom that define the distribution.

Figure 26 T.DIST.RT function.

Where:

• You input the calcuated t-statistic as “x”
• deg_freedom is the number of degree of freedom

This function is used when we are testing if a sample mean is significantly greater than a hypothesised value.

In our marketing campaign case, we found that our t-statistic = 2.643.

We can use this function to find p-value: =T.DIST.RT(2.643, 79)

This yields a p-value of approximately 0.005, indicating strong evidence that the campaign increased purchases.

After exploring how you can calculate p-values for upper-tailed t-tests, it is important to understand that Microsoft Excel also offers a specific function for determining p-values in lower-tailed t-tests. You will find this function particularly valuable when you need to assess whether a sample mean is significantly less than a hypothesised value. Excel’s built-in capabilities will streamline your process, allowing you to perform efficient and accurate statistical analysis without resorting to manual calculations.

You will encounter lower-tailed t-tests in various research scenarios where you focus on determining if a sample statistic is significantly lower than a population parameter. For example, in quality control, you might test whether the mean weight of a product is significantly less than the specified standard. In medical research, you could investigate whether a new treatment reduces symptoms significantly more than an existing treatment.

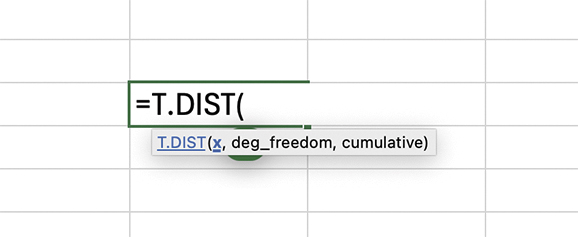
Lower-Tailed (One-Tailed) t-Test:

Formula: =T.DIST(x, deg_freedom, cumulative)

Figure 27 T.DIST function

Show description|Hide description

The image shows the Excel function T.DIST, which calculates the Student’s t-distribution. It requires three inputs: x (the value to evaluate), deg_freedom (the degrees of freedom), and cumulative (a logical value that determines the type of distribution returned).

Figure 27 T.DIST function

Where:

• You input the calcuated t-statistic as “x”
• deg_freedom is the number of degree of freedom
• cumulative is set to “TRUE”

This function is used when we are testing if a sample mean is significantly less than a hypothesised value.

A negative t-statistic is used because we are looking at the lower tail of the distribution.

Having explored both upper-tailed and lower-tailed t-tests, you should now turn your attention to two-tailed t-tests. Microsoft Excel continues to support your statistical analysis needs by offering a function that enables you to calculate p-values for two-tailed t-tests efficiently. This type of test broadens your analytical capabilities, as you will find it particularly useful when you need to determine whether a sample mean differs significantly from a hypothesised value in either direction, without specifying a particular tail of the distribution.

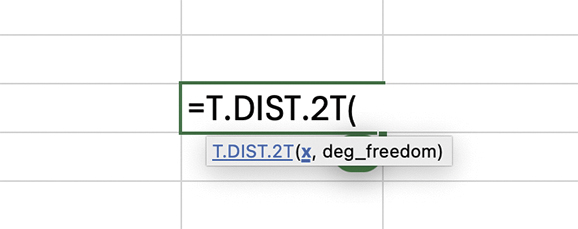
Two-Tailed t-Test:

Formula: =T.DIST.2T(x, deg_freedom)

Where:

• You input the absolute value of calcuated t-statistic as “x”
• deg_freedom is the number degree of freedom

Figure 28 T.DIST.2T function

Show description|Hide description

The image shows the Excel function T.DIST.2T, which calculates the two-tailed probability of the Student’s t-distribution. The function takes two inputs: x (the t-statistic value) and deg_freedom (the degrees of freedom).

Figure 28 T.DIST.2T function

This function is used when we are testing if a sample mean is significantly different (either higher or lower) from a hypothesised value. We use the absolute value of the t-statistic because we are considering both tails of the distribution.