3.4 Multiple uses of representations
Of course, it is rarely possible to identify a single category for any given representation, because in practice representations are multipurpose. I have identified individual categories for each of the drawings in Figure 11 , but this is not entirely realistic and it is possible to argue that every drawing belongs in more than one category. For example, I have categorised the drawing in Figure 11c as a drawing for describing because it includes details which can be used to realise the design. But the drawing also represents a detailed level of thinking about the concept, and can be used for communicating this thinking to others within a design team. So I could just as easily categorise it as a drawing for communicating and a drawing for thinking. But, even though representations may be multipurpose, they are not omnipurpose. Not all representations can be used for all purposes. Representations can play a dual role in shaping how we understand a concept, and how we can manipulate it. The decisions we make in modelling a concept have consequences in terms of our understanding and potential for manipulation.
Take, as an example, a circle, which we could represent in many different ways: we could represent it visually as an outline; we could represent it constructively using a piece of string attached to a post on one end and with a pencil on the other; or we could represent it mathematically as an equation defined according to (x, y) coordinates in a Cartesian plane.
Each of these representations gives us a different view of what a circle is:
- a separation of space into two distinct regions
- the outcome of a physical construction
- a set of coordinates.
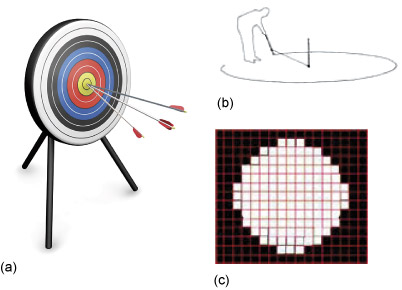
These different views are all useful in different situations. For example, separation of space is a useful representation for an archer who wants to ensure their arrows land in the inner region rather than the outer region of a target (Figure 15a); the physical construction recipe is useful for a builder marking out a circular area for a patio (Figure 15b); the mathematical representation is useful for graphical computing, and enables a graphical algorithm to identify which pixels on a screen are part of the circle (Figure 15c).
These different views allow us to understand and apply the concept of a circle in different ways, appropriate to different tasks. They also give us different opportunities for modifying the concept. If the circle is an outline separating two areas of space, then we can move the circle and change where the separation lies. If it is a construction, then we can change its dimensions by changing the length of the piece of string. If it is an equation, then we can manipulate the variables in the equation so that we can change both the position and size of the circle. The different representations give rise to different acceptable manipulations, and also allow us to conceptualise these differently. For example the construction and the equation both allow us to change the size of the circle, but the construction allows us to understand this physically, while the equations are more abstract.
The dual role that representations play in shaping how we view concepts, and how we can manipulate them, means that it is important to consider which representations to use for a given purpose. To review the representations we have considered in the course so far:
- Drawings are fast, cheap and flexible. But they are two-dimensional, and require interpretation into a detailed model for embodiment processes such as layout and analysis.
- Concept diagrams can be quick to produce, and represent aspects of a vision that can’t be captured figuratively in drawings; but they are abstract, and do not describe form.
- Physical models, made from card, foam, clay, wood, etc., are flexible and three-dimensional; but they require interpretation into a detailed model for embodiment processes such as analysis.
- Digital models are easily imported into embodiment processes, but are time consuming to produce, and are inflexible in structure.
Activity 7 Choosing appropriate representations
Which representations would you use for the following activities?
- Sharing a vision within a design meeting.
- Presenting a vision to a client.
- Discussing a vision with a craftsman who will build a prototype.
Use the textbox to record your answer.
Answer
Your answers may be different from mine, but what is important is that representations are chosen that are suitable for the task at hand. I have opted for the following representations:
- I would use a paper-based representation in a design meeting, such as a sketch or a concept diagram. These can be used to communicate intent and are easy to annotate and label with changes that record outcomes of the meeting.
- I would use a model to present to a client, either a CAD or a physical model. A CAD model would allow me to simulate different scenarios, whereas a physical model would allow the client to experience the vision tangibly.
- I would use a CAD model or detailed drawings to discuss a vision with a craftsman. These would be complete with details of dimensions and would provide different views, to ensure that there is no ambiguity and that the prototype accurately reflects my vision.