6.1 Crystal symmetry
When you first look at a collection of minerals in a museum, there may seem to be an infinite variety of crystal shapes. However, on closer inspection there is an underlying order, and this is best seen by the consistency in the angles between crystal faces for particular groups of minerals. Crystals possess a variety of symmetries, and it has been demonstrated by X-ray methods that symmetry visible in hand specimen relates to the internal arrangement of atoms.
Most people have an idea of what is meant by symmetry, as many everyday objects and living things possess it. There are two main types of symmetry:
- reflection symmetry, where one side of an object is the mirror image of the other side (e.g. insects, birds and spoons)
- rotational symmetry, where an object looks the same after a certain amount of rotation (e.g. many flowers, starfish and bicycle wheels).
Many complicated patterns such as carpet or wallpaper designs have symmetry, but these can sometimes be a little difficult to discern. Consider, therefore, an object with obvious symmetry, such as a snowflake (Figure 27).

Each snowflake can be rotated by 60° about an axis perpendicular to the page and it will look exactly the same as it did before. The operation can be repeated six times in a full 360° rotation, and at each 60° interval the snowflake will look the same. Thus the snowflake has a six-fold rotational symmetry. A snowflake also possesses reflection symmetry: if you 'split' the snowflakes along certain planes, called mirror planes, the two halves are mirror images of each other.
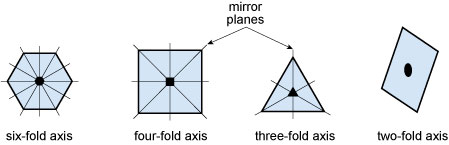
Some examples of rotational and reflection symmetry found in crystals are illustrated in Figure 28. The first three shapes are bisected with examples of mirror planes to illustrate reflection symmetry. Placed at the centre of each shape is the appropriate symbol for their rotation axis.