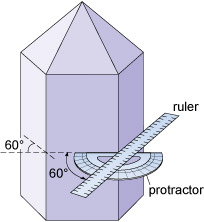
6.3 Crystal systems
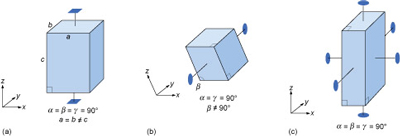
Most three-dimensional lattices display some symmetry, although the symmetry elements (e.g. rotation axes and mirror planes) can be in any direction. Some arrangements of symmetry elements place special constraints on the shape of the unit cell. For example, a four-fold rotation axis requires the unit cell to have a square section at right angles to the symmetry axis (Figure 31a). Three four-fold axes at right angles to each other imply that the unit cell must be a cube, and so on.
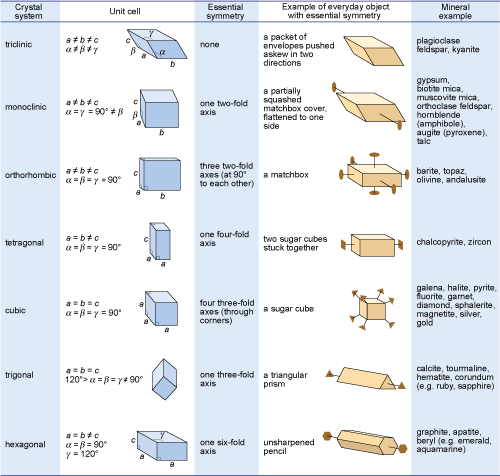
Crystals are classified on the basis of this three-dimensional symmetry (and hence the shapes of their unit cells) into one of seven different crystal systems (Figure 32).
Study the three unit cell shapes shown in Figure 31. To which of the seven crystal systems would each belong?
Figure 31a: tetragonal; Figure 31b: monoclinic (note that while two axes are at 90° to each other, one axis is inclined - hence the term 'monoclinic'); Figure 31c: orthorhombic. See Figure 32.
What would be the shape of the cross-section, at right angles to the longest side, of a crystal with a unit cell like that in Figure 31a?
The cross-section would be square.
The beauty of crystallography is that you do not need to see the lattice, the unit cell, or the atoms in order to deduce this symmetry. The extent of symmetry varies from the cubic system, which has the most symmetry, to triclinic, which has the least.
Generally, the more symmetry a crystal has, the more constraints this places on its external shape. Crystals belonging to the cubic system tend to have equidimensional shapes, such as cubes, octahedra (with eight faces), or rather rounded-looking crystals with many faces (e.g. dodecahedra, with 12 faces). Pyrite and galena, for example, can have very simple cube-shaped crystals, which clearly indicate their underlying cubic symmetry. These same minerals may also have more complex shapes, with many more faces, but each shape still has the symmetry that places the mineral within the cubic system.
The same possibility for variation within certain limits applies to other minerals in different crystal systems. Despite their complexity, by focusing on the symmetry relationships between faces, you may still be able to determine the crystal system.
Sometimes a crystal has less symmetry than first appearance suggests. For example, quartz crystals are usually prismatic, and often have a hexagonal appearance in cross-section. At first, quartz thus appears to have a six-fold rotation axis. However, in some well-developed quartz crystals there are a number of small faces that present the same appearance only three times in a full 360° rotation, revealing that the true symmetry is less.
Given this information, to which crystal system does quartz belong?
The trigonal system (Figure 32), as this is the only system in which only one three-fold axis is present.
It is important to realise that conditions during the growth of a crystal often prevent some faces from developing as perfectly as they might, which results in individual crystal faces having different sizes. Some crystal faces may not be developed at all. Therefore, when looking at crystal symmetry, the angles between faces should be considered (Figure 33), not the absolute sizes of individual faces.