4.3 Ekman drift
The obvious way to observe whether the oceans move in the direction of the winds is to follow a floating object. Early Arctic explorers noted that icebergs did not drift exactly in the direction of the winds, but 20-40° to the right of the wind direction. The Swedish mathematician Vagn Ekman developed a theory of wind-driven ocean currents to explain this observation. He started with the theoretical idea of an infinitely deep and wide ocean with no variations in density and imagined the ocean as a series of infinite horizontal layers.
A wind will move the surface through wind stress, but the surface is then acted upon by the Coriolis force and so is deflected to the right (in the Northern Hemisphere). This moving surface layer is also acted upon by friction with its lower surface - the eddy viscosity - and the layer underneath starts to move. But the transfer of momentum by friction is an inefficient process and the energy transferred is greatly reduced. This means that when the forces are in balance, the speed of the second layer down will be much less than that of the top layer. In the second layer the balance of forces means that it too is deflected to the right by the Coriolis force. This second layer is in contact with the deeper third layer and exactly the same processes happen there, and so on.
The result is that the energy transferred downwards significantly decreases with each layer and, more importantly, each layer will be deflected progressively to the right (in the Northern Hemisphere). The consequent rotation pattern in the upper layers of the ocean is called the Ekman spiral (Figure 17). The total depth of the frictional influence of the wind is called the Ekman layer.
Ekman found that, in his ideal ocean, the direction of the surface current will be approximately 45° to the right of the wind direction in the Northern Hemisphere, and 45° to the left of the wind direction in the Southern Hemisphere. A limitation of Ekman's theory is that the oceans are not infinitely wide and deep and that the eddy viscosity (that is, the friction between successive layers) varies with depth.
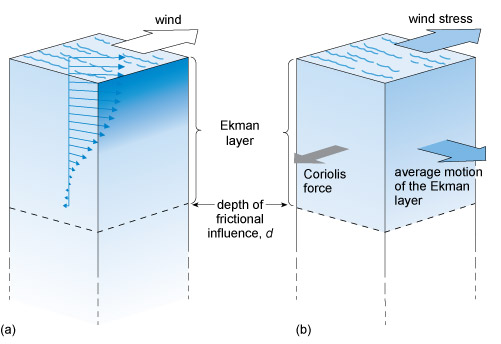
The most important point about Ekman's theory is that there is a layer of water (shown in Figure 17) at the surface (not necessarily the same thickness as the mixed layer) which is influenced by the wind and moves with a mean current called the Ekman drift over the depth of the Ekman layer. This is to the right of the wind direction in the Northern Hemisphere and the left in the Southern Hemisphere. Under typical conditions the depth of the Ekman drift is strongly influenced by the thickness of the mixed layer and is largely dependent on the time of year and wind speed, typically varying from tens of metres up to 200 m.
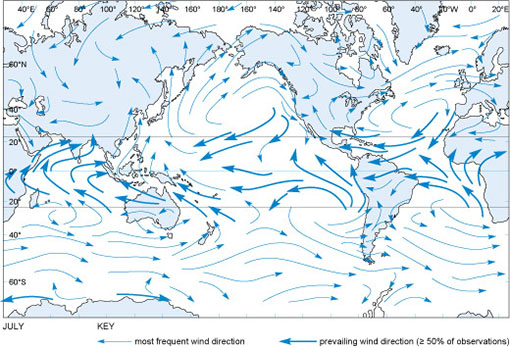
From the Ekman drift velocity and the depth over which it acts, the total transport of water due to the Ekman drift, called the Ekman transport, can be calculated. Armed with this basic theory of the wind-driven surface circulation, you can now investigate the effect of the global surface winds (Figure 18) on the oceans.
Figure 18 compares well with the map of mean surface currents in Figure 15. Where surface currents join in continuous circulation patterns as in the North Atlantic, the effect of the Ekman drift is striking.