2.1 Arwynebedd siapiau syml
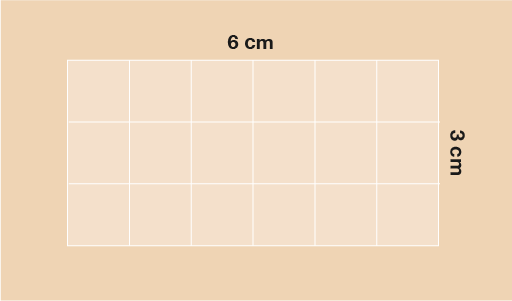
Wrth edrych ar arwynebedd, y siapiau symlaf i ddechrau gyda nhw yw sgwariau a phetryalau. Os ydych chi’n edrych ar y petryal yn Ffigur 13 gallwch weld ei fod yn 6 cm o hyd a 3 cm o led. Os ydych chi’n cyfrif y sgwariau, mae 18 ohonyn nhw. 18 cm2 yw arwynebedd y siâp.
Nid yw bob amser yn bosibl (neu’n ymarferol) cyfrif y sgwariau mewn siâp neu ofod ond mae’n ddarlun defnyddiol i’ch helpu i ddeall beth yw arwynebedd.
Yn fwy ymarferol, i ganfod arwynebedd (A) sgwâr neu betryal, byddech yn lluosi’r hyd (h) â’r lled (ll), felly’r fformiwla fyddai:
Arwynebedd = hyd × lled neu:
A =h× ll (cofiwch nad yw’r arwydd lluosi’n cael ei ysgrifennu fel arfer mewn fformiwla)
Yn yr enghraifft isod A = 6 × 3 = 18 cm2.
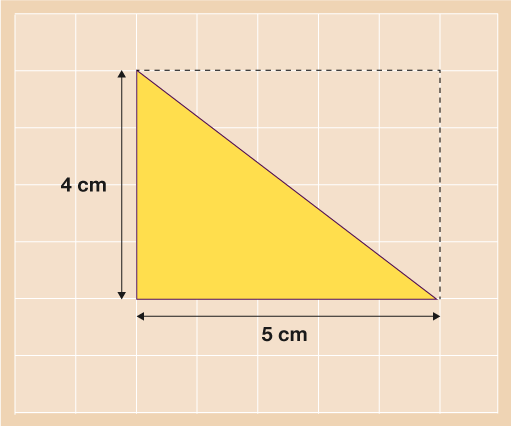
Mae triongl yn siâp arall lle gallwch ganfod yr arwynebedd yn gymharol syml. Os meddyliwch am driongl, mewn gwirionedd dim ond hanner petryal ydyw. Mae hyn i’w weld hawsaf gyda thriongl ongl sgwâr fel y dangosir isod. Gallwch weld bod y triongl (mewn melyn) yn betryal sydd wedi cael ei dorri yn ei hanner ar letraws.
Er mwyn canfod arwynebedd y triongl, felly, rydych chi’n lluosi’r sail â’r uchder (fel y byddech chi’n gwneud ar gyfer petryal) ac yna’n haneru’r ateb.
Weithiau dangosir hyn fel y fformiwla:
A = (s × u) ÷ 2
lle mai s yw sail y triongl a u yw’r uchder fertigol.
Gellir ysgrifennu’r fformiwla hon fel:
A =
Ar gyfer y triongl isod felly, byddech yn gwneud:
A = (5 × 4) ÷ 2
A = 20 ÷ 2
A = 10 cm2
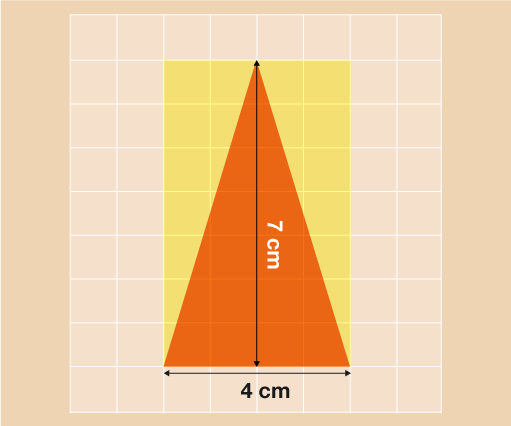
Mae’r fformiwla hon yn aros yr un peth ar gyfer unrhyw driongl. Edrychwch ar y triongl isod. Mae ychydig yn llai amlwg na gyda’r enghraifft uchod, ond pe baech chi’n tynnu’r ddwy adran felen ac yn eu rhoi at ei gilydd, byddech chi’n cael siâp o’r un faint yn union â’r triongl oren.
Gellir canfod arwynebedd y triongl hwn yn yr un ffordd â’r un blaenorol:
- A = (s × u) ÷ 2
- A = (4 × 7) ÷ 2
- A = 28 ÷ 2
- A = 14 cm2
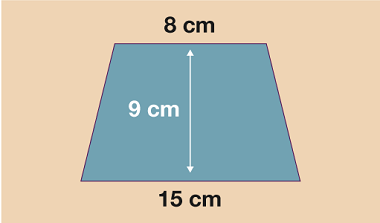
Siâp arall y bydd angen ichi ganfod ei arwynebedd, o bosibl, yw’r trapesiwm. Bydd angen ichi ddefnyddio fformiwla syml ar gyfer y siâp hwn (peidiwch â mynd i banig pan welwch chi hi, mae’n edrych yn frawychus ond mae’n eithaf hawdd ei defnyddio mewn gwirionedd!)
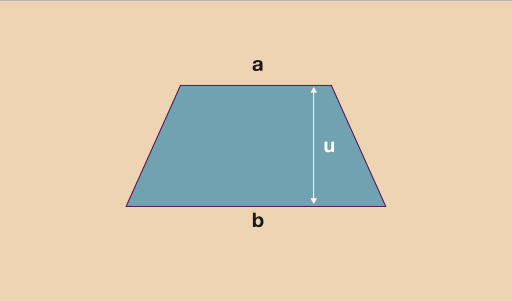
Mae trapesiwm yn edrych fel unrhyw un o’r siapiau isod.

Er mwyn gweithio allan arwynebedd trapesiwm y cwbl mae angen ichi wybod yw’r uchder fertigol a hyd yr ochrau top a gwaelod. Yn draddodiadol, ‘a’ yw’r enw ar hyd y top, ‘s’ yw hyd y gwaelod ac ‘u’ yw’r uchder fertigol. Unwaith mae hyn yn eglur gallwch wedyn ddefnyddio’r fformiwla:
A =
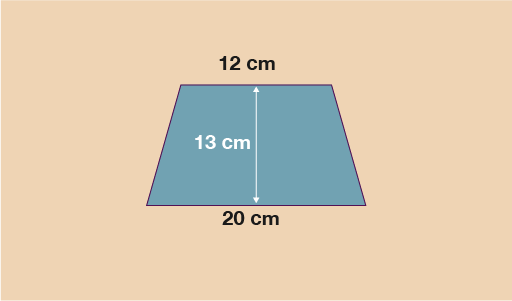
Dewch inni edrych ar enghraifft o sut i weithio allan arwynebedd y trapesiwm isod. Gallwn weld bod yr hyd top (a) = 12 cm. Mae’r hyd gwaelod (b) = 20 cm, ac mae’r uchder (u) = 13 cm.
Gan ddefnyddio’r gwerthoedd hyn a’r fformiwla:
A =
A =
A =
A = 208 cm2
Nawr eich bod wedi gweld sut i weithio allan arwynebedd nifer o siapiau sylfaenol, mae’n bryd rhoi prawf ar eich sgiliau. Rhowch gynnig ar y gweithgaredd isod. Cofiwch, fel gyda pherimedr, cyn ichi ddechrau gwneud unrhyw gyfrifiadau mae’n rhaid ichi wneud yn siŵr bod yr holl fesuriadau yn yr un unedau.
Gweithgaredd 4: Canfod yr arwynebedd
Ateb
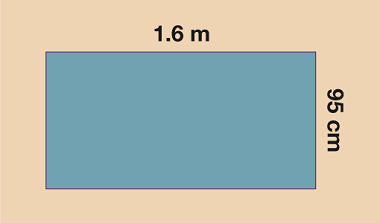
Mae angen ichi drosi’r mesuriadau i’r un unedau cyn y gallwch weithio allan yr arwynebedd.
Os ydych chi’n gweithio mewn cm:
1.6 m = 160 cm, felly
A = 160 × 95 = 15 200 cm2
Os ydych chi’n gweithio mewn m:
95 cm = 0.95 m, felly
A = 1.6 × 0.95 = 1.52 m2
Ateb
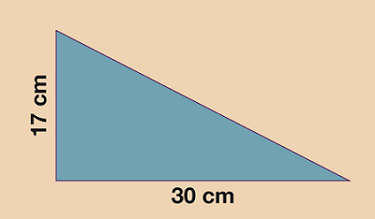
- Y ddau fesuriad mae arnom eu hangen ar gyfer y triongl yw’r sail (30 cm) a’r uchder fertigol (17 cm). Peidiwch â chael eich twyllo gan yr hyd ar letraws sef 46 cm, nid oes arnoch ei angen ar gyfer yr arwynebedd!
- A = (s × u) ÷ 2
- A = (30 × 17) ÷ 2
- A = 510 ÷ 2
- A = 255 cm2
Ateb
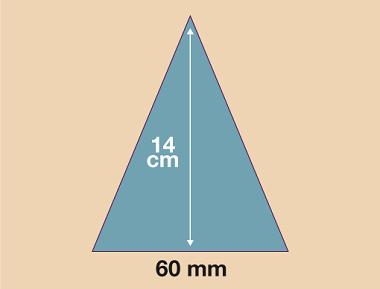
Mae angen ichi drosi’r mesuriadau i’r un unedau cyn y gallwch weithio allan yr arwynebedd.
Os ydych chi’n gweithio mewn mm: 14 cm = 140 mm
- A = (s × u) ÷ 2
- A = (60 × 140) ÷ 2
- A = 8400 ÷ 2
- A = 4200 mm2
- Os ydych chi’n gweithio mewn cm: 60 mm = 6 cm
- A = (s × u) ÷ 2
- A = (6 × 14) ÷ 2
- A = 84 ÷ 2
- A = 42 cm2
Nawr eich bod wedi meistroli canfod arwynebedd siapiau sylfaenol, mae’n bryd edrych ar siapiau cyfansawdd.
Mae siâp cyfansawdd yn siâp sydd wedi’i wneud o fwy nag un siâp sylfaenol. Anaml iawn y gwelwch ofod llawr, darn o ardd neu wal sy’n gwbl betryal. Yn amlach na pheidio bydd yn gyfuniad o siapiau. Y newyddion da yw, er mwyn canfod arwynebedd siapiau cyfansawdd, rydych chi’n eu rhannu i’w siapiau sylfaenol, yn canfod arwynebedd pob un o’r rhain, ac yna’n eu hadio ar y diwedd!