Sgipio i'r cynnwys
Mynd i'r prif gynnwys
header search
ahihi OpenLearn
OpenLearn
Menu
sticky search

Ynghylch y cwrs am ddim hwn

Dewch yn fyfyriwr gyda’r Brifysgol Agored

Lawrlwytho'r cwrs hwn

Rhannu'r cwrs am ddim hwn

Cynnwys y cwrs Cynnwys y cwrs
Mathemateg bob dydd 2
Mathemateg bob dydd 2

Dechrau'r cwrs am ddim hwn nawr. Crëwch gyfrif a mewngofnodwch. Ymrestrwch a chwblhewch y cwrs am ddatganaid o'ch cyfranogiad neu fathodyn digidol am ddim os ydynt ar gael.

Mwy o gyrsiau am ddim

7 Tebygolrwydd

Byddwch yn defnyddio tebygolrwydd yn rheolaidd yn eich bywyd pob dydd:

  • Ddylech chi fynd ag ambarél gyda chi heddiw?
  • Pa mor debyg yw hi y bydd y bws yn brydlon?
  • Pa mor debyg yw hi y byddwch yn bodloni’r terfyn amser?
Described image
Ffigur 26 Tebygolrwydd – rydych yn debyg o fod yn ei ddefnyddio’n barod
Show description|Hide description

Cartŵn tebygolrwydd o ddau ddisgybl y tu allan i swyddfa’r Pennaeth. Mae’r capsiwn yn darllen ‘Byddai’n well gen i tasen ni heb ddysgu tebygolrwydd achos ’dyw hi ddim yn debyg o fynd yn dda inni’.

Ffigur 26 Tebygolrwydd – rydych yn debyg o fod yn ei ddefnyddio’n barod

Mae tebygolrwydd yn ymwneud â pha mor debyg, neu annhebyg, yw hi y bydd rhywbeth yn digwydd. Er enghraifft, pan fyddwch yn taflu darn arian, mae’r siawns y bydd yn glanio ar y pen yn one divided by two neu 50% neu 0.5 (ydych chi’n cofio’ch gwaith yn Sesiwn 1 ynghylch trosi ffracsiynau, degolion a chanrannau i’w gilydd?).

Efallai ei bod hi’n haws mynegi’r tebygolrwydd y bydd digwyddiad yn digwydd fel ffracsiwn i ddechrau. Yna, os ydych eisiau ei fynegi fel canran neu ddegolyn, gallwch ei drosi.

Dewch inni edrych ar enghraifft.

Enghraifft: Tebygolrwydd siocled

Mewn bocs o siocledi mae 15 darn o siocled llaeth, 5 darn o siocled tywyll a 10 darn o siocled gwyn. Os yw’r bocs yn llawn ac rydych yn dewis darn o siocled ar hap, beth yw’r tebygolrwydd y byddwch yn dewis darn o siocled tywyll?

Dull

Mae 5 darn o siocled tywyll yn y bocs. Mae cyfanswm o 15 + 5 + 10 = 30 o ddarnau o siocled yn y bocs.

Felly’r tebygolrwydd o ddewis darn o siocled tywyll yw:

five divided by 30 = one divided by six

Gellid gofyn hefyd beth yw’r tebygolrwydd o ddewis naill ai darn o siocled tywyll neu ddarn o siocled gwyn. Ar gyfer hyn mae angen cyfanswm y darnau tywyll a’r darnau gwyn:

5 + 10 = 15

Nid yw cyfanswm nifer y darnau o siocled yn y bocs yn newid, felly’r tebygolrwydd o ddewis naill ai darn o siocled tywyll neu ddarn o siocled gwyn yw:

15 divided by 30 = one divided by two

Gellid hyd yn oed gofyn beth yw’r tebygolrwydd na fydd digwyddiad yn digwydd. Er enghraifft, y tebygolrwydd na fyddwch yn dewis darn o siocled gwyn. Yn yr achos hwn, cyfanswm nifer y darnau o siocled nad ydynt yn wyn yw 15 + 5 = 20.

Unwaith eto, nid yw cyfanswm nifer y darnau o siocled yn y bocs yn newid, felly’r tebygolrwydd o beidio â dewis darn o siocled gwyn yw:

20 divided by 30 = two divided by three

Nawr rhowch gynnig arni trwy gwblhau’r gweithgaredd byr isod.

Gweithgaredd 17: Cyfrifo tebygolrwydd

  1. Rydych yn prynu pecyn o falŵns aml-liw ar gyfer parti plant. Mae gennych 26 o falŵns coch, 34 o falŵns gwyrdd, 32 o falŵns melyn a 28 o falŵns glas.

    Rydych yn tynnu balŵn o’r pecyn heb edrych. Beth yw’r tebygolrwydd y byddwch yn dewis balŵn gwyrdd?

    Rhowch eich ateb fel ffracsiwn yn ei ffurf symlaf.

  2. Gwerthwyd 350 o docynnau raffl yn ffair y pentref. Mae 20 o docynnau yn ennill gwobr. Beth yw’r tebygolrwydd na fyddwch yn ennill gwobr yn y raffl?

    Rhowch eich ateb fel canran wedi’i thalgrynnu i ddau le degol.

Ateb

  1. Mae 34 o falŵns gwyrdd. Cyfanswm nifer y balŵns yw 26 + 34 + 32 + 28 = 120.

    Felly’r tebygolrwydd o ddewis balŵn gwyrdd yw:

    • 34 divided by 120 = 17 divided by 60 yn ei ffurf symlaf.

  2. Os oes 20 o docynnau sy’n ennill gwobr, mae 350 − 20 = 330 o docynnau nad ydynt yn ennill gwobr.

    Fel ffracsiwn: 330 divided by 350

    Er mwyn trosi i ganran, rydych yn gwneud 330 ÷ 350 × 100 = 94.29% wedi’i thalgrynnu i ddau le degol.

Er mwyn trosi i ganran, rydych yn gwneud 330 ÷ 350 × 100 = 94.29% wedi’i thalgrynnu i ddau le degol.

Weithiau bydd angen ichi gyfrifo’r tebygolrwydd y bydd mwy nag un peth yn digwydd. Yn yr achos hwn, gallai’r digwyddiadau fod:

  • yn annibynnol – sy’n golygu nad yw canlyniad un digwyddiad yn effeithio ar y llall

  • yn ddibynnol – sy’n golygu bod canlyniad un digwyddiad yn effeithio ar y llall.

Yn y naill achos neu’r llall, gallwch ddefnyddio diagramau cangen neu dablau i’ch helpu i ddatrys y problemau hyn.

Enghraifft: Tebygolrwydd rhywedd

Os yw cwpl yn cael dau o blant, ni fydd rhywedd y plentyn cyntaf yn effeithio ar rywedd yr ail blentyn. Gellir dangos yr holl bosibiliadau ar ffurf tabl:

  • B = bachgen

    M = merch

Tabl 27 Tebygolrwydd rhywedd plentyn cyntaf ac ail blentyn
    HighlightedPlentyn cyntaf
    HighlightedB HighlightedM
Highlighted

Ail

blentyn

 HighlightedB BB MB
HighlightedM BM MM

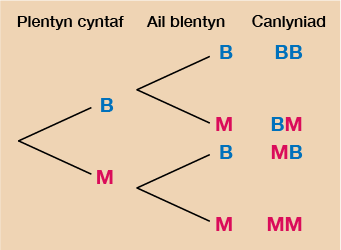
Fel arall, gellir ei ddangos fel diagram cangen:

Described image
Ffigur 27 Diagram cangen yn dangos canlyniadau rhywedd plentyn cyntaf ac ail blentyn
Show description|Hide description

Mae’r graffigyn yn dangos tair colofn ar draws y top wedi’u labelu (o’r chwith i’r dde) ‘Plentyn cyntaf’, ‘Ail blentyn’ a ‘Canlyniad’. Yn y golofn ‘Plentyn cyntaf’ ceir y llythrennau B (bachgen) ac M (merch). Mae dwy linell yn mynd o ‘B’ yn y golofn ‘Plentyn cyntaf’ i ‘B’ ac ‘M’ yn y golofn ‘Ail blentyn’. Mae dwy linell yn mynd o ‘M’ yn y golofn ‘Plentyn cyntaf’ i ‘B’ ac ‘M’ arall yn y golofn ‘Ail blentyn’. Mae’r golofn ‘Canlyniad’ yn dangos y canlyniadau posibl, un o dan y llall: BB, BM, MB, MM.

Ffigur 27 Diagram cangen yn dangos canlyniadau rhywedd plentyn cyntaf ac ail blentyn

Mae’r tabl a’r diagram cangen yn dangos bod pedwar o bosibiliadau:

  1. BB – bachgen yna bachgen arall

  2. BM – bachgen yna merch

  3. MB – merch yna bachgen

  4. MM – merch yna merch arall

O’r holl bosibiliadau, mae siawns 1 mewn 4 neu one divided by four (1 chwarter/25%) o gael dau fachgen neu ddwy ferch.

Mae siawns 2 mewn 4 two divided by four ( one divided by two /1 hanner/50%) o gael un plentyn yr un o’r ddau rywedd.

Gweithgaredd 18: Defnyddio diagramau a thablau i gyfrifo tebygolrwydd

  1. Cwblhewch y manylion sydd ar goll yn y diagram cangen canlynol:

    Described image
    Ffigur 28 Diagram cangen yn dangos canlyniadau taflu darn arian dwywaith
    Show description|Hide description

    Mae’r graffigyn yn dangos tair colofn wedi’u labelu (o’r chwith i’r dde) ‘Darn arian 1’, ‘Darn arian 2’ a ‘Canlyniad’. Yn y golofn ‘Darn arian 1’ ceir y llythrennau P (pen) ac C (cynffon). Mae dwy linell yn mynd o ‘P’ yn y golofn ‘Darn arian 1’ i ‘P’ ac ‘C’ yn y golofn ‘Darn arian 2’. Mae dwy linell arall yn mynd o ‘C’ yn y golofn ‘Darn arian 1’ i ‘P’ ac ‘C’ arall yn y golofn ‘Darn arian 2’. Mae’r golofn ‘Canlyniad’ yn dangos ‘?(a)’, yna ‘PC’, yna ‘?(b)’ ac yna ‘?(c)’.

    Ffigur 28 Diagram cangen yn dangos canlyniadau taflu darn arian dwywaith

  2. Lluniadwch dabl yn dangos yr holl bosibiliadau pan deflir dau ddarn arian.

  3. Beth yw’r tebygolrwydd o daflu dwy gynffon?

Ateb

  1.  

    • a.PP

    • b.CP

    • c.CC

  2. Dylai’ch tabl edrych fel yr un isod.

Tabl 28 Tabl tebygolrwydd taflu darn arian
    HighlightedDarn arian 1
    HighlightedP HighlightedC
Highlighted

Darn

arian 2

 HighlightedP PP CP
HighlightedC PC CC

  1. O’r holl bosibiliadau, mae siawns 1 mewn 4 neu one divided by four (1 chwarter/25%) o gael 2 gynffon.

Pan fyddwch yn gwirio’ch atebion, cofiwch efallai eich bod wedi defnyddio dull gwahanol i ateb y cwestiwn. Mewn arholiad, mae’n bwysig dangos eich gwaith cyfrifo, gan y byddwch yn gallu ennill marciau hyd yn oed os na fydd eich ateb yn gywir.

Erbyn hyn rydych wedi cwblhau Sesiwn 4 o’ch cwrs. Llongyfarchiadau!

Crynodeb

Yn yr adran hon, rydych wedi dysgu:

  • mai tebygolrwydd digwyddiad yw pa mor debygol neu annhebygol yw hi y bydd yn digwydd, a gellir mynegi hyn fel ffracsiwn, degolyn neu ganran.
  • sut i ddefnyddio tabl neu ddiagram cangen i ddangos canlyniadau gwahanol dau ddigwyddiad neu fwy.