Course content Course content

Prices, location and spread

Start this free course now. Just create an account and sign in. Enrol and complete the course for a free statement of participation or digital badge if available.

More free courses

2.3 More than two numbers

The idea of a weighted mean can be extended to more than two numbers. To see how the calculation is done in general, remind yourself first how we calculated the weighted mean of two numbers and with corresponding weights and .

Multiply each number by its weight to get the products and .
Sum these products to get .
Sum the weights to get .
Divide the sum of the products by the sum of the weights.

This leads to the following formula.

Weighted mean of two or more numbers

The weighted mean of two or more numbers is

This is the formula which is used to find the weighted mean of any set of numbers, each with a corresponding weight.

Example 12 A weighted mean of wine prices

Suppose we have the following three batches of wine prices (in pence per bottle).

We want to calculate the weighted mean of these three batch means using, as corresponding weights, the three batch sizes. Rather than applying the formula directly, the calculations can be set out in columns.

Table 4 Data on wine purchases
Batch	Number (batch mean)	Weight (batch size)	Number weight ( = product)
Batch 1	525.5	6	3 153.0
Batch 2	468.0	2	936.0
Batch 3	504.2	12	6 050.4
Sum		20	10 139.4

The weighted mean is

We round this to the same accuracy as the original means, to get a weighted mean of 507.0. (Note that this lies between 468.0 and 525.5. This is a useful check, as a weighted mean always lies within the range of the original means.)

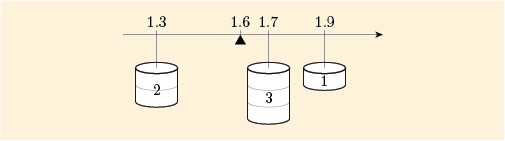
The physical analogy in Example 12 can be extended to any set of numbers and weights. Suppose that you calculate the weighted mean for:

This is given by

This is pictured in Figure 11, with the point of balance for these three weights shown at 1.6.

Figure 11 Point of balance for three means

Show description|Hide description

Point of balance for three means. The figure shows a horizontal arrow pointing to the right. Four suitably spaced points are marked on it, 1.3, 1.6, 1.7 and 1.9. Immediately below 1.6 there is a solid arrow head pointing upwards, which is the fulcrum or balancing point of the balance. Suspended from the point marked 1.3 is a pile of 2 discs, suspended from the point marked 1.7 is a pile of 3 discs and suspended from the point marked 1.9 is a single disc.

Point of balance for three means

You will meet many examples of weighted means of larger sets of numbers in Subsection 5.2, but we shall end this section with one more example.

Example 13 Weighted means of many gas prices

Example 11 showed the calculation of a weighted mean of gas prices using, for simplicity, just the two cities London and Edinburgh. We can extend Example 11 to calculate a weighted mean of all 14 gas prices from Table 3, using as weights the populations of the 14 cities. The calculations are set out in Table 5.

Table 5 Product of gas price and weight by city
City	Price (p/kWh):	Weight:	Price weight:
Aberdeen	3.740	19	71.060
Edinburgh	3.740	42	157.080
Leeds	3.776	150	566.400
Liverpool	3.801	82	311.682
Manchester	3.801	224	851.424
Newcastle-upon-Tyne	3.804	88	334.752
Nottingham	3.767	67	252.389
Birmingham	3.805	228	867.540
Canterbury	3.796	5	18.980
Cardiff	3.743	33	123.519
Ipswich	3.760	14	52.640
London	3.818	828	3161.304
Plymouth	3.784	24	90.816
Southampton	3.795	30	113.850
Sum		1834	6973.436

The entries in the weight column, , are the approximate populations, in 10 000s, of the urban areas that include each city (as measured in the 2001 Census). For each city, we multiply the price, , by the weight, , to get the entry in the last column, .

The weighted mean of the gas prices using these weights is then

or, in symbols,

As and , the weighted mean is

So the weighted mean of these gas prices, using approximate population figures as weights, is 3.802p per kWh.

Note that this weighted mean is larger than all but three of the gas prices for individual cities. That is because the cities with the two highest populations, London and Birmingham, also have the highest gas prices, and the weighted mean gas price is pulled towards these high prices.

Although the details of the calculation above are written out in full in Table 5, in practice, using even a simple calculator, this is not necessary. It is usually possible to keep a running sum of both the weights and the products as the data are being entered. One way of doing this is to accumulate the sum of the weights into the calculator’s memory while the sum of the products is cumulated on the display. If you are using a specialist statistics calculator, the task is generally very straightforward. Simply enter each price and its corresponding weight using the method described in your calculator instructions for finding a weighted mean.

Activity 8 Weighted means on your calculator

Use your calculator to check that the sum of weights and sum of products of the data in Table 5 are, respectively, 1834 and 6973.436, and that the weighted mean is 3.802. (No solution is given to this activity.)

Activity 9 Weighted mean electricity price

Table 6 is similar to Table 5, but this time it presents the average price of electricity, in pence per kilowatt hour (kWh). These data are again for the year 2010 for typical consumers on credit tariffs in the same 14 cities we have been considering for gas prices, with the addition of Belfast. Again, the weights are the approximate populations of the relevant urban areas, in 10 000s.

Table 6 Populations and electricity prices in 15 cities
City	Price (p/kWh):	Weight:
Aberdeen	13.76	19
Belfast	15.03	58
Edinburgh	13.86	42
Leeds	12.70	150
Liverpool	13.89	82
Manchester	12.65	224
Newcastle-upon-Tyne	12.97	88
Nottingham	12.64	67
Birmingham	12.89	228
Canterbury	12.92	5
Cardiff	13.83	33
Ipswich	12.84	14
London	13.17	828
Plymouth	13.61	24
Southampton	13.41	30
Sum

Use these data to calculate the weighted mean electricity price. (Your calculator will almost certainly allow you to do this without writing out all the values in the column.)

Discussion

The table showing the required sums (and the values in the column, that you may not have had to write down), is as follows.

City	Price (p/kWh):	Weight:	Price weight:
Aberdeen	13.76	19	261.44
Belfast	15.03	58	871.74
Edinburgh	13.86	42	582.12
Leeds	12.70	150	1 905.00
Liverpool	13.89	82	1 138.98
Manchester	12.65	224	2 833.60
Newcastle-upon-Tyne	12.97	88	1 141.36
Nottingham	12.64	67	846.88
Birmingham	12.89	228	2 938.92
Canterbury	12.92	5	64.60
Cardiff	13.83	33	456.39
Ipswich	12.84	14	179.76
London	13.17	828	10 904.76
Plymouth	13.61	24	326.64
Southampton	13.41	30	402.30
Sum		1892	24 854.49

Thus , and

So the weighted mean of electricity prices is 13.14p per kWh.

Previous 2.2 Further uses of weighted means

Next Exercises on Section 2

Take your learning further

Making the decision to study can be a big step, which is why you’ll want a trusted University. We’ve pioneered distance learning for over 50 years, bringing university to you wherever you are so you can fit study around your life. Take a look at all Open University courses.

If you’re new to university-level study, read our guide on Where to take your learning next, or find out more about the types of qualifications we offer including entry level Access modules, Certificates, and Short Courses.

Want to achieve your ambition? Study with us and you’ll be joining over 2 million students who’ve achieved their career and personal goals with The Open University.

Browse all Open University courses

My OpenLearn Profile

About this free course

Become an OU student

Download this course

Share this free course