5.1 What are the CPI and RPI?

The CPI and the RPI are the main measures used in the UK to record changes in the level of the prices most people pay for the goods and services they buy. The RPI is intended to reflect the average spending pattern of the great majority of private households. Only two classes of private households are excluded, on the grounds that their spending patterns differ greatly from those of the others: pensioner households and high-income households. The CPI, however, has a wider remit – it is intended to reflect the spending of all UK residents, and also covers some costs incurred by foreign visitors to the UK.

The CPI and RPI are calculated in a similar way to the price index for Gradgrind Ltd’s energy in Section 4. However, they are calculated once a month rather than just once a year, and are based on a very large ‘basket of goods’. The contents of the basket and the weights assigned to the items in the basket are updated annually to reflect changes in spending patterns (as was the case with Gradgrind’s index for energy prices), and the index is ‘chained’ to previous values. However, once decided on at the beginning of the year, the contents of the basket and their weights remain fixed throughout the year.

For the RPI, the price ratio for the basket each month is calculated relative to the previous January. Then the value of the index is obtained by multiplying the value of the index for the previous January by this price ratio. For example,

The CPI works in much the same way, except that price ratios are calculated relative to the previous December. So, for example,

Since these price indices are calculated from price ratios, they measure price changes in terms of the ratio of the overall level of prices in a given month to the overall level of prices at an earlier date. In practice, data on most prices are collected on a particular day near the middle of the month; the values of the RPI and CPI calculated using these data are referred to simply as the values of the RPI and CPI for the month. For example, the RPI took the value 239.9 in February 2012. This value measures the ratio of the overall level of prices in February 2012 to the overall level of prices on a date at which the index was fixed at its starting value of 100. This date, called a base date, is 13 January 1987 (at the time of writing). Thus the general level of prices in February 2012, as measured by the RPI, was times the general level of prices in January 1987. The base date has no significance other than to act as a reference point. (The CPI base date is 2005 and this refers to the average level of prices throughout 2005, not to a specific date in 2005.)

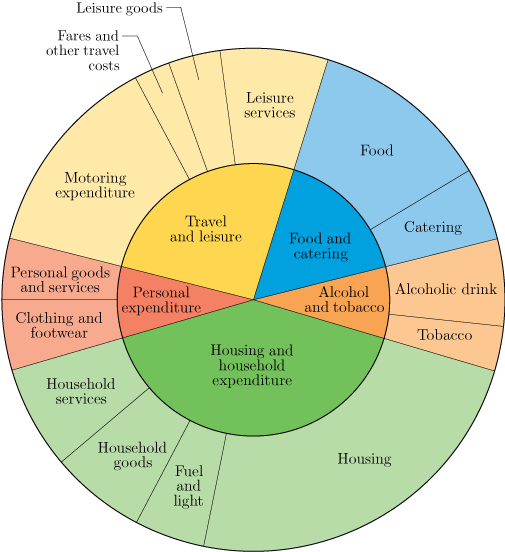
The RPI and CPI are each based on a very large ‘basket’ of goods and services. (The two baskets are similar, but not exactly the same.) Each contains around 700 items including most of the usual things people buy: food, clothes, fuel, household goods, housing, transport, services, and so on. Each basket is an ‘average’ basket for a broad range of households. The items in the baskets are often grouped into broader categories. For the RPI, the five fundamental groups are: ‘Food and catering’, ‘Alcohol and tobacco’, ‘Housing and household expenditure’, ‘Personal expenditure’ and ‘Travel and leisure’. These groups are divided into 14 more detailed subgroups (which are further divided into sections), as shown in Figure 37. The items in the CPI basket are divided into 12 broad groupings called divisions, which are further subdivided.

Figure 37 Structure of the RPI in 2012 (based on data from the Office for National Statistics)

Show description|Hide description

Two concentric circles showing the structure of the Retail Prices Index in 2012, based on data from www.ons.gov.uk. The inner circle shows 5 sectors, representing the 5 fundamental groups of goods and services, each with their own colour. The biggest sector, making an angle of about 150 degrees at the centre, is coloured green and represents Housing and household expenditure. Reading round the circle clockwise from that sector there is a small sector, making an angle of about 30 degrees, coloured red and labelled Personal expenditure. The next sector, making an angle of approximately 90 degrees at the centre, is coloured yellow and labelled Travel and leisure. The next sector, making an angle of approximately 60 degrees at the centre, and coloured dark blue, is labelled Food and catering. The last sector, making an angle of about 30 degrees at the centre is labelled Alcohol and tobacco. The outer circle forms a concentric ring round the inner circle. Each of the sectors in the inner circle is subdivided in the ring, to show a breakdown of the relevant type of expenditure. The colour coding continues, but the colours in the outer ring are paler than those in the inner circle.

Housing and household expenditure is divided into four. These are 1 housing, 2 fuel and light, 3 household goods and 4 household services, with housing accounting for about half the expenditure in this sector. Personal expenditure is split into two approximately equal parts, 1 clothing and footwear and 2 personal goods and services. Travel and leisure is split into four parts. The first and largest of these, accounting for about half the expenditure in this sector, is labelled motoring expenditure. The second is fares and other travel costs and the third is leisure goods, which together amount to about the same expenditure as the fourth part, leisure services. ‘Food and catering’ is divided into two, separating food from catering, with the part labelled catering being less than half that of food. Alcohol and tobacco is split between the two, with alcohol being almost twice the size of tobacco.

Structure of the RPI in 2012 (based on data from the Office for National Statistics)

The inner circle shows the five groups, and the outer ring shows the 14 subgroups. Notice that in the inner circle the sector labelled ‘Food and catering’ has been drawn almost twice as large (as measured by area) as that labelled ‘Alcohol and tobacco’. This reflects the fact that the typical household spends nearly twice as much on food and catering as on alcohol and tobacco. The weight of an item or group reflects how much money is spent on it. So the weight of the ‘Food and catering’ group is almost twice that of ‘Alcohol and tobacco’.

The outer ring represents the same total expenditure as the inner circle, but in more detail. For example, in the outer ring the area labelled ‘Food’ (which mostly consists of food bought for use in the home) is more than twice as large as that labelled ‘Catering’ (which includes meals in restaurants and canteens, and take-away meals and snacks), reflecting the fact that the typical household spends more than twice as much on food as on catering; the weight of the subgroup ‘Food’ is more than double the weight of the subgroup ‘Catering’. The chart gives a good indication of average spending patterns in the UK in the early 21st century.

To ensure that the basket of goods for the index reflects the proportion of average spending devoted to different types of goods and services, it is necessary to find out how people actually spend their money. The Living Costs and Food Survey (LCF) records the spending reported by a sample of 5000 households spread throughout the UK. Data from the LCF are used to calculate the weights of most of the items included in the RPI basket. Since 1962, the weights have been revised each year, so that the index is always based on a basket of goods and services that is as up to date as possible. Because of this regular weight revision, the index is chained (as was the Gradgrind Ltd index).

(Most of the weights for the CPI come from a different source, the UK National Accounts, though in turn this source is partly based on data from the LCF. Again, the weights are revised each year.)

The weight of a group or subgroup directly depends on the average expenditure of households on that item. In Subsection 2.1, you saw that it is only the relative size of the weights that affects the value of the weighted mean – this is Rule 1 for weighted means. So instead of using the average expenditure of an item as its weight, the expenditure figures for the items can all be multiplied by the same factor to produce a new, more convenient, set of weights. For the RPI, this factor is chosen so that the sum of the weights is 1000. Table 12 shows the 2012 weights used in the RPI for the groups and subgroups. Notice that each group weight is obtained by summing the weights for its subgroups.

The following checklist provided contains the major categories of goods and services included in the RPI. In the next activity, you will be asked to complete the last three columns of this checklist to make rough estimates of your household’s group weights.

Maximise

Figure 38 A checklist for one household’s average monthly expenditure

Show description|Hide description

A checklist for one household’s average monthly expenditure. An opportunity to compare your monthly expenditure with that of a two-person household. The table consists of the RPI groups and subgroups in the first column. There are then 3 columns under a general heading ‘Expenditure and weights’. The columns are headed ‘Expenditure 2012 in pounds sterling’, ‘Group totals in pounds sterling’ and ‘Group weights’. There is then a vertical line and there are three more columns under the general heading ‘Your expenditure and weights’. These 3 columns are also headed ‘Expenditure 2012 in pounds sterling’, ‘Group totals in pounds sterling’ and ‘Group weights’ and there are lines to indicate where entries should be made. However, there are no entries in these three columns. They have been left blank for you to input your own data.

The entries for the two-person data are as follows. Under the group heading Food and catering there are 3 subgroups. At home has an expenditure of 370. Canteen, snacks and takeaways has an expenditure of 80 and restaurant meals has an expenditure of 20. Together these give a group total of 470, which is written in the next column, on the row below. Level with this and under the column headed Group weights is written 266.

In a similar way, under the group heading Alcohol and tobacco there are 2 subgroups. Alcoholic drink has an expenditure of 8 and cigarettes and tobacco has no expenditure. The group total is therefore 8 and the weight is given as 5.

Under the group heading Housing and household expenditure there are 10 subgroups. Mortgage interest forward slash rent has an expenditure of 82. Council tax has an expenditure of 95. Water charges have an expenditure of 47 and household insurance has an expenditure of 29. Repairs, maintenance or DIY has an expenditure of 40. Gas, electricity, coal or oil bills has an expenditure of 210.

Household goods, which includes furniture, appliances and consumables etc has an expenditure of 70. Telephone and internet cost 20. There was no expenditure for school and university fees or for pet care. In total, this group Housing and household expenditure had a group total of 593 and a group weight of 336.

Under the group heading Personal expenditure clothing and footwear had an expenditure of 45 and other, which included hairdressing, chemists’ goods etc, had expenditure of 10. Together they have a group total of 55 and a group weight of 31.

There are 8 subgroups under the group Travel and leisure. Motoring, which includes purchase, maintenance, petrol, tax and insurance, had expenditure of 210. Fares had expenditure of 200. Books, newspapers and magazines had expenditure of 80. Audio-visual equipment, CDs etc had expenditure of 15. Toys, photographic and sports goods had expenditure of 3, while TV purchase or rental and licence had no expenditure. Cinema, theatre etc had expenditure of 30 and holidays had expenditure of 100. Together these give a group total of 638 and a weight of 362.

Under the group totals is a total for all the groups, which is 1764 and under the group weights the total is 1000.

A checklist for one household’s average monthly expenditure

The figures already in the checklist were completed for a two-person household. Some of the figures were accurate, others were necessarily very rough estimates. Nevertheless, the household’s weights give a reasonable indication of the proportion of the household’s expenditure (in 2012) on the five main groups used in the RPI.

The total expenditure was £1764. So the group weights were calculated by multiplying all the group total expenditures by a constant factor of 1000/1764, to ensure the weights sum to 1000. The weight for ‘Food and catering’, for example, is

Another way to calculate this is to multiply the proportion of monthly expenditure spent on food and catering by 1000. The proportion is

Since the total weight is 1000, the weight for ‘Food and catering’ is

Notice that the group weights for this particular household differ quite considerably from those used in the RPI in 2012 (see Table 12). For instance, a much greater proportion of expenditure is on ‘Food and catering’ and a much smaller proportion is spent on ‘Alcohol and tobacco’.