2.1 The mean of a combined batch
This first subsection looks at how a mean can be calculated when two unequally weighted batches are combined.
Example 7 Alan’s and Beena’s biscuits
Suppose we are conducting a survey to investigate the general level of prices in some locality. Two colleagues, Alan and Beena, have each visited several shops and collected information on the price of a standard packet of a particular brand of biscuits. They report as follows (Figure 9).
Alan visited five shops, and calculated that the mean price of the standard packet at these shops was 81.6p.
Beena visited eight shops, and calculated that the mean price of the standard packet at these shops was 74.0p.
If we had all the individual prices, five from Alan and eight from Beena, then they could be amalgamated into a single batch of 13 prices, and from this combined batch we could calculate the mean price of the standard packet at all 13 shops. However, our two investigators have unfortunately not written down, nor can they fully remember, the prices from individual shops. Is there anything we can do to calculate the mean of the combined batch?
Fortunately there is, as long as we are interested in arithmetic means. (If they had recorded the medians instead, then there would have been very little we could do.)
The mean of the combined batch of all 13 prices will be calculated as
We already know that the size of the combined batch is the sum of the sizes of the two original batches; that is, . The problem here is how to find the sum of the combined batch of Alan’s and Beena’s prices. The solution is to rearrange the familiar formula
so that it reads
This will allow us to find the sums of Alan’s five prices and Beena’s eight prices separately. Adding the results will produce the sum of the combined batch prices. Finally, dividing by 13 completes the calculation of finding the combined batch mean.
Let us call the sum of Alan’s prices ‘sum(A)’ and the sum of Beena’s prices ‘sum(B)’.
For Alan: and , so .
For Beena: and , so .
For the combined batch:
Here, the result has been rounded to give the same number of digits as in the two original means.
The process that we have used above is an important one. It will be used several times in the rest of this course. The box below summarises the method, using symbols.
Mean of a combined batch
The formula for the mean of a combined batch is
where batch consists of batch combined with batch , and
For our survey in Example 7,
The formula summarises the calculations we did as
This expression is an example of a weighted mean. The numbers 5 and 8 are the weights. We call this expression the weighted mean of 81.6 and 74.0 with weights 5 and 8, respectively.
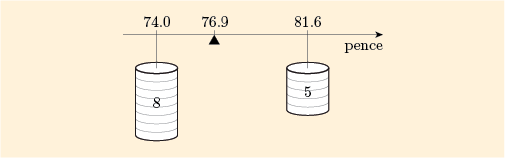
To see why the term weighted mean is used for such an expression, imagine that Figure 10 shows a horizontal bar with two weights, of sizes 5 and 8, hanging on it at the points 81.6 and 74.0, and that you need to find the point at which the bar will balance. This point is at the weighted mean: approximately 76.9.
This physical analogy illustrates several important facts about weighted means.
It does not matter whether the weights are 5 kg and 8 kg or 5 tonnes and 8 tonnes; the point of balance will be in the same place. It will also remain in the same place if we use weights of 10 kg and 16 kg or 40 kg and 64 kg – it is only the relative sizes (i.e. the ratio) of the weights that matter.
The point of balance must be between the points where we hang the weights, and it is nearer to the point with the larger weight.
If the weights are equal, then the point of balance is halfway between the points.
This gives the following rules.
Rules for weighted means
Rule 1 The weighted mean depends on the relative sizes (i.e. the ratio) of the weights.
Rule 2 The weighted mean of two numbers always lies between the numbers and it is nearer the number that has the larger weight.
Rule 3 If the weights are equal, then the weighted mean of two numbers is the number halfway between them.
Example 8 Two batches of small televisions
Suppose that we have two batches of prices (in pounds) for small televisions:
To find the mean of the combined batch we use the formula above, with
This gives
Note that this is the weighted mean of 119 and 185 with weights 7 and 13 respectively. It lies between 119 and 185 but it is nearer to 185 because this has the greater weight: 13 compared with 7.
Example 8 is the subject of the following screencast. [Note that references to ‘the unit’ and ‘the units’ should be interpreted as ‘this course’. The original wording refers to the Open University course from which this material is adapted.]