2 World-views

2.2 The clockwork Universe

2.2.1 Mechanics and determinism

It is probably fair to say that no single individual has had a greater influence on the scientific view of the world than Isaac Newton. The main reason for Newton's prominence was his own intrinsic genius, but another important factor was the particular state of knowledge when he was, in his own phrase, 'in the prime of my age for invention'.

In 1543, a century before Newton's birth. Nicolaus Copernicus launched a scientific revolution by rejecting the prevailing Earth-centred view of the Universe in favour of a heliocentric view in which the Earth moved round the Sun. By removing the Earth, and with it humankind, from the centre of creation, Copernicus had set the scene for a number of confrontations between the Catholic church and some of its more independently minded followers. The most famous of these must surely have been Galileo, who was summoned to appear before the Inquisition in 1633, on a charge of heresy, for supporting Copernicus' ideas. As a result Galileo was 'shown the instruments of torture', and invited to renounce his declared opinion that the Earth moves around the Sun. This he did, though tradition has it that at the end of his renunciation he muttered 'Eppur si muove' ('And yet it moves').

Figure 5 Three views of planetary motion, (a) The Earth-centred view of the ancient Greeks and of the Catholic church in the sixteenth century. (b) The Copernican system, in which the planets move in collections of circles around the Sun. (c) The Keplerian system, in which a planet follows an elliptical orbit, with the Sun at one focus of the elIipse.

In the Protestant countries of Northern Europe, thought on astronomical matters was more free, and it was there in the early seventeenth century, that the German-born astronomer Johannes Kepler (1571-1630) devised a modified form of Copernicanism that was in good agreement with the best observational data available at the time. According to Kepler, the planets did move around the Sun, but their orbital paths were ellipses rather than collections of circles. This discovery, first published in 1609 in Kepler's book Astronomia Nova (The New Astronomy), was essentially an observational result. Kepler had no real reason to expect that the planets would move in ellipses, though he did speculate that they might be impelled by some kind of magnetic influence emanating from the Sun.

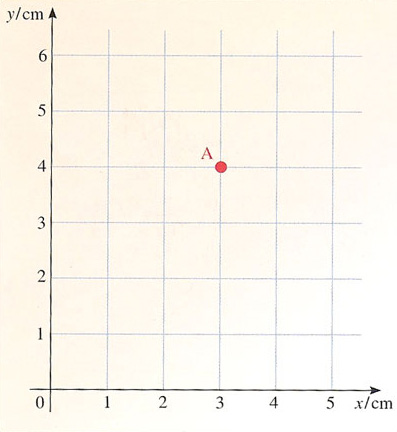
Kepler's ideas were underpinned by new discoveries in mathematics. Chief among these was the realisation, by René Descartes, that problems in geometry can be recast as problems in algebra. Like most revolutionary ideas, the concept is disarmingly simple. Imagine a giant grid extending over the whole of space. Figure 6 shows the two-dimensional case, with a grid extending over part of the page. The grid is calibrated (in centimetres) so the position of any point can be specified by giving its x- and y-coordinates on the grid. For example, the coordinates of point A are x = 3 cm and y = 4 cm.

Figure 6 A two-dimensional coordinate system can be used to locate the position of any point in terms of its x- and y-coordinates

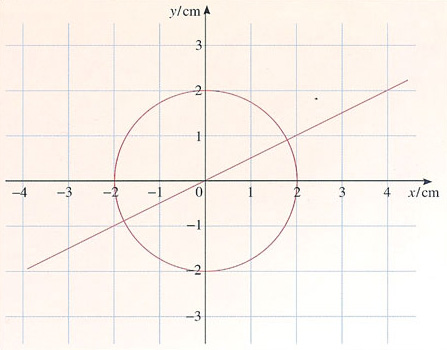
This idea becomes more powerful when we consider lines and geometrical shapes. The straight line shown in Figure 7 is characterised by the fact that, at each point along the line, the y-coordinate is half the x-coordinate. Thus, the x- and y-coordinates of each point on the line obey the equation y = 0.5x, and this is said to be the equation of the line. Similarly, the circle in Figure 7 is characterised by the equation = 2 cm. This is the beginning of a branch of mathematics, called coordinate geometry, which represents geometrical shapes by equations, and which establishes geometrical truths by combining and rearranging those equations. Sometimes, what is difficult to show using traditional geometry is easy to establish using algebra, so this 'mapping' of geometry into algebra gave scientists new ways of tackling geometrical problems, allowing them to go further than the greatest mathematicians of ancient Greece.

Figure 7 A two-dimensional coordinate system can be used to represent lines and other geometrical shapes by equations

Newton's good fortune was to be active in physics (or 'natural philosophy' as it would then have been called) at a time when the cause of Kepler's ellipses was still unexplained and the tools of geometry were ripe for exploitation. The physics of Aristotle was clearly inadequate, and all other attempts seemed unconvincing. The new astronomy called for a new physics which Newton had the ability and the opportunity to devise. He was the right man, in the right place, at the right time.

Isaac Newton (1642-1727)

Figure 8 Isaac Newton

Isaac Newton was born on Christmas Day 1642 at Woolsthorp in Lincolnshire, England. His father had died a few months before the birth and Newton himself was born so prematurely that it was thought he might not survive. Newton was partly brought up by his grandmother, and seems not to have had a close relationship with his mother. He exhibited no great talent at school, but managed to avoid the task of managing his mother's farmlands and became instead an undergraduate at Trinity College in the University of Cambridge.

Figure 9 Woolsthorp Manor - Newton's birthplace

As a student Newton read the works of Aristotle and was taught mathematics, as was customary, but he also taught himself physics and thus became acquainted with the works of Galileo and Kepler, amongst others. He graduated in 1665, by which time he had already started to break new ground in mathematics. Due to an outbreak of plague, the University of Cambridge was closed for much of the next two years and Newton spent most of his time back at Woolsthorp. It was during this period that he made many of his greatest breakthroughs, or at least laid their foundations. Over an eighteen month period he:

• made fundamental advances in mathematics (essentially creating the subject of calculus, which has become a major part of the language of physics);

• used a glass prism to demonstrate that white light is actually a mixture of colours;

• began to consider the possibility that gravity, which obviously influenced bodies close to the Earth, might be a universal phenomenon holding the Moon in its orbit around the Earth and the Earth in its orbit around the Sun.

Following the reopening of the University, Newton returned to Trinity College where he became a Fellow in 1667. Two years later, still only 26, he was appointed Lucasian Professor of Mathematics on the recommendation of his predecessor, Isaac Barrow.

Figure 10 Trinity College, Cambridge around 1690

In addition to combining mathematical genius and profound physical insight, Newton also possessed practical skills. He built the furnaces in his own small laboratory in Trinity College, where he personally carried out alchemical experiments. He also constructed a novel kind of reflecting telescope, for which he was elected a Fellow of the Royal Society. However, Newton was a solitary and difficult person who has often been described as neurotic. He reacted badly to criticism and expected to get full credit for his discoveries even though he often did little to publicise them. He became involved in a number of bitter disputes over priority. Newton also harboured unconventional religious views (he was essentially a Unitarian) which prevented him from becoming the Master of his college. In 1678 he apparently suffered a nervous breakdown and for several years thereafter concentrated on alchemy and scriptural studies.

Newton was recalled to natural philosophy in 1684 by the young astronomer Edmond Halley who asked how a planet would move if it was attracted towards the Sun by a force that weakened in proportion to the inverse square of its distance from the Sun: in symbols, force ∝ 1/(distance)². (This means, for example, that increasing the distance by a factor of three decreases the force by a factor of nine.) Newton is said to have immediately told Halley the answer (an ellipse) having worked it out during the plague years. Halley persuaded Newton to recreate his calculations and publish them. The result, in 1686, was what is widely regarded as the most influential book in the history of science. Newton's Philosophiae Naturalis Principia Mathematica (Mathematical Principles of Natural Philosophy), a work usually referred to simply as Principia. In the opening pages of this book, Newton presented his definitions of force and mass, and his three laws of motion. He then went on to demonstrate that a body attracted towards a fixed point by a force that varied in proportion to the inverse square of its distance from that point would, in many circumstances, follow an elliptical path. After establishing many other results Newton presented, in Part 3 of the book, his System of the World in which he proposed that gravity was a universal force, acting between any two particles of matter, with a magnitude that is proportional to the product of their masses and the inverse square of their separation - just the kind of inverse square law that Halley had asked about. Thus Newton was able to explain the observed motion of the planets. He went on to consider the Moon's motion in detail (taking account of the gravitational influence of both the Earth and the Sun), the behaviour of comets, and the gravitational origin of the Earth's oceanic tides. The scope and power of Principia caused a sensation, and made Newton the foremost scientist of his time, or perhaps any time.

Figure 11Principia - Newton's masterpiece

Newton suffered another breakdown in 1693 and subsequently quit Cambridge and the academic life in favour of London and the world of affairs. He became Warden of the Mint in 1696 and successfully oversaw the introduction of a new coinage. As a consequence he was appointed to a lucrative position as Master of the Mint and devoted much of his remaining time to theology and biblical chronology. He was elected President of the Royal Society in 1703, published his last great scientific work Opticks in 1704 (based on work performed many years earlier), and was knighted in 1705. He died, in London in 1727, and is buried in Westminster Abbey.

For years before Newton, people had been trying to understand the world from a scientific perspective, discovering laws that would help explain why things happen in the way that they do. Bits of knowledge were assembled, but there was no clear idea how these bits related to one another; understanding was fragmentary. Newton's great achievement was to provide a synthesis of scientific knowledge. He did not claim to have all the answers, but he discovered a convincing quantitative framework that seemed to underlie everything else. For the first time, scientists felt they understood the fundamentals, and it seemed that future advances would merely fill in the details of Newton's grand vision. Before Newton, few could have imagined that such a world-view would be possible. Later generations looked back with envy at Newton's good fortune. As the great Italian-French scientist Joseph Lagrange remarked:

At the core of Newton's world-view is the belief that all the motion we see around us can be explained in terms of a single set of laws. We cannot give the details of these laws now, but it is appropriate to mention three key points:

1. Newton concentrated not so much on motion, as on deviation from steady motion - deviation that occurs, for example, when an object speeds up, or slows down, or veers off in a new direction.

2. Wherever deviation from steady motion occurred, Newton looked for a cause. Slowing down, for example, might be caused by braking. He described such a cause as a force. We are all familiar with the idea of applying a force, whenever we use our muscles to push or pull anything.

3. Finally Newton produced a quantitative link between force and deviation from steady motion and, at least in the case of gravity, quantified the force by proposing his famous law of universal gravitation.

In keeping with his grand vision, Newton proposed just one law for gravity - a law that worked for every scrap of matter in the Universe, for moons and planets as well as for apples and the Earth. By combining this law with his general laws of motion, Newton was able to demonstrate mathematically that a single planet would move around the Sun in an elliptical orbit, just as Kepler claimed each of the planets did. Moreover, thanks to the understanding that gravity was the cause of planetary motion, Newtonian physics was able to predict that gravitational attractions between the planets would cause small departures from the purely elliptical motion that Kepler had described. In this way, Newton was able to explain Kepler's results and to go beyond them.

In the hands of Newton's successors, notably the French scientist Pierre Simon Laplace (1749-1827), Newton's discoveries became the basis for a detailed and comprehensive study of mechanics (the study of force and motion). The upshot of all this was a mechanical world-view that regarded the Universe as something that unfolded according to mathematical laws with all the precision and inevitability of a well-made clock. The detailed character of the Newtonian laws was such that once this majestic clockwork had been set in motion, its future development was, in principle, entirely predictable. This property of Newtonian mechanics is called determinism. It had an enormously important implication. Given an accurate description of the character, position and velocity of every particle in the Universe at some particular moment (i.e. the initial condition of the Universe), and an understanding of the forces that operated between those particles, the subsequent development of the Universe could be predicted with as much accuracy as desired.

Figure 12 An orrery (a mechanical model of the Solar System) can be taken as a metaphor for the clockwork Universe of Newtonian mechanics

Needless to say, obtaining a completely detailed description of the entire Universe at any one time was not a realistic undertaking, nor was solving all the equations required to predict its future course. But that wasn't the point. It was enough that the future was ordained. If you accepted the proposition that humans were entirely physical systems, composed of particles of matter obeying physical laws of motion, then in principle, every future human action would be already determined by the past. For some this was the ultimate indication of God: where there was a design there must be a Designer, where there was a clock there must have been a Clockmaker. For others it was just the opposite, a denial of the doctrine of free will which asserts that human beings are free to determine their own actions. Even for those without religious convictions, the notion that our every thought and action was pre-determined in principle, even if unpredictable in practice, made the Newtonian Universe seem strangely discordant with our everyday experience of the vagaries of human life.