2.2.2 Energy and conservation
Newtonian mechanics is concerned with explaining motion, yet it contains within it the much simpler idea that some things never change. Take the concept of mass, for example, which appears throughout Newtonian mechanics, including the law of gravitation. In Newtonian mechanics, mass is conserved. This means that the mass of the Universe is constant and the mass of any specified collection of particles is constant, no matter how much rearrangement occurs within the system. A chemist might take one kilogram of hydrogen and let it react with eight kilograms of oxygen to produce water. According to the law of conservation of mass, nine kilograms of water will be produced, the same as the total mass of the ingredients (1 kg + 8 kg = 9 kg). You may think this is trivial, but it is not. Conservation laws are rare and wonderful things. There is no general law of conservation of volume for example. The initial volume of the hydrogen and oxygen is far greater than the final volume of the water. The fact that mass is conserved really is a deep discovery about the checks and balances that exist in our Universe.
Newtonian mechanics introduced several other important conservation laws, including the celebrated law of conservation of energy. Not too surprisingly, this law states that the total energy of the Universe is constant and the total energy of an isolated system of particles is constant. But the full meaning of these words will only become apparent once the concept of energy has been properly defined.
For the moment, it is sufficient to note that we all have some familiarity with the concept of energy. We pay money for gas, electricity and petrol precisely because they are sources of energy, and we use that energy to heat and light our homes and to drive cars. From this, it is apparent that energy has many different forms - chemical energy in gas or electrical energy can be converted into light energy, thermal energy, or the energy of a whirring vacuum cleaner. It is possible to change energy from one form into another but, crucially, when all these forms are properly quantified, the total amount of energy remains constant. Energy is neither created nor destroyed because it is a conserved quantity.
Perhaps the simplest form of energy is kinetic energy: the energy associated with motion. If a particle has mass m and speed v, its kinetic energy is given by the formula

Suppose the particle hits a wall and is brought to a sudden halt. It then has no speed and no kinetic energy, but the initial energy has not been lost. Rather, it has been converted into other forms of energy, such as those associated with sound and heat.
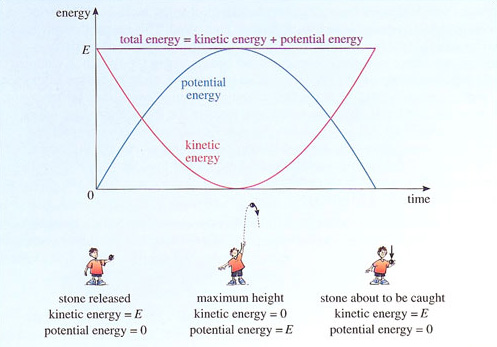
The conservation of energy can be illustrated by considering a stone that is thrown vertically upwards. The stone starts out with a certain amount of kinetic energy, but as it climbs it slows down and its kinetic energy decreases. What happens to this energy? The answer is that there is another form of energy called potential energy, which in this case is associated with the downward pull of gravity and increases as the stone climbs. On the upward part of its journey, the stone's kinetic energy is gradually converted into potential energy until, at the top of its flight, the stone is momentarily at rest. At this point, the stone has no kinetic energy and its potential energy is at its highest. On the way down, potential energy is converted back into kinetic energy, as the stone loses height and gains speed. Assuming that no other forms of energy are involved, by the time the stone returns to its initial height, all of its initial kinetic energy is recovered and the stone is once again travelling at its initial speed. Figure 13 shows how the kinetic and potential energies of the stone vary during its up-and-down flight. The total energy, formed by adding the kinetic and potential energies together, is also shown. You can see quite clearly that energy is converted from one form to another while the total energy remains fixed.
One of the consequences of the conservation of energy is that it makes sense to think of storing energy in order to have a ready supply whenever required. Figure 14 shows several examples of energy storage in action.

