5.1 The prosecutor’s fallacy

Judges and juries that are not comfortable with numbers may be at risk of misinterpreting them. A stark example of this is the so-called ‘prosecutor’s fallacy’. This is where the probability of a particular scientific test is mistakenly assumed to be the same as the probability of guilt.

Because the prosecutor’s fallacy is quite a tricky idea to understand, the following activity will guide you through the idea in a series of small steps.

Activity 5 The prosecutor’s fallacy

Timing: Allow about 30 minutes

Read through the following scenario and answer the questions as you progress.

Part 1

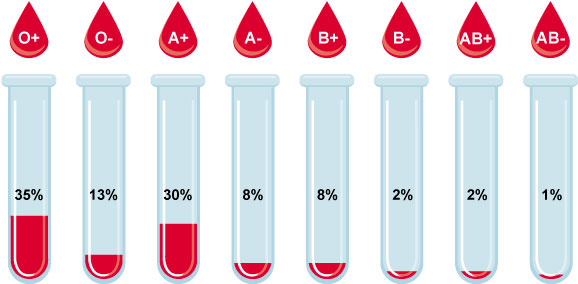
Imagine a scenario in which a burglary has been committed. Blood recovered from the scene of the burglary is type AB−, which is possessed by one person in a hundred or 1% of the population of the UK (see Figure 14 for the distribution of blood types in the UK).

Josip has been arrested. He was in the area where the burglary was committed at the time it was committed and has blood type AB−.

Figure 14 Proportion of blood types in the UK’s population

Show description|Hide description

An image of a series of eight test tubes of blood filled with the proportion of blood types in the UK population: O+ (35%), O− (13%), A+ (30%), A− (8%), B+ (8%), B− (2%), AB+ (2%), and AB− (1%).

Figure 14 Proportion of blood types in the UK’s population

1. If this is the only evidence, what would you estimate the probability that Josip committed the burglary is? Once you have made your selection, remember to click ‘Save response’. Once you have saved your response, you can compare your view with that of other learners taking this course. The results of the poll are displayed by clicking the discussion tab below.

Active content not displayed. This content requires JavaScript to be enabled.

Interactive feature not available in single page view (see it in standard view).

Comment

The results of the poll are displayed below. You may need to refresh your browser to load the results.

Active content not displayed. This content requires JavaScript to be enabled.

Interactive feature not available in single page view (see it in standard view).

Select the answer for

Part 2

here

Next, imagine that Emma, a police detective constable, calculates that around 10,000 people were in the area during that time and had the opportunity to commit the burglary.

2. Now what would you say the probability that Josip committed the burglary?

More than 99%

99%

Less than 99%

Difficult to say

 

a. 

More than 99%

b. 

99%

c. 

Less than 99%

d. 

Difficult to say

The correct answer is c.

Discussion

You may have been tempted for the poll at the outset to choose 99%, but that would have been to ignore how many people could have committed the crime, a number sometimes called the ‘base rate’. The correct answer at that stage would have been ‘difficult to say’, as you were not given the base rate. Given the further information that 10,000 people had the opportunity and one person in a hundred has this blood type, then statistically, it is likely that there would be 100 from this group who test positive (this is calculated by dividing 10,000 by 100). The probability of Josip being involved is, therefore, only 1 in 100, 1%, or 0.01. Without the base rate information, it is difficult to say how likely it was that they committed the crime. Only with the base rate information can you give a figure.

In summary, this activity should have demonstrated that the prosecutor’s fallacy (the idea that the probability of a positive test is the same as the probability of guilt) is often unsafe. There are a lot of other pieces of information, and assumptions, that you need to be aware of before you can make any assessment of guilt.

Do not feel bad if you did fall for the prosecutor’s fallacy. It even happens to experts who should know better. In R v Deen,^{Footnote 29} the Court of Appeal quashed a conviction in a rape case for precisely this reason. The DNA expert had said the probability of a positive test was 1 in 3 million and then made the mistake of concluding that the likelihood of the DNA coming from anybody other than Andrew Deen was also 1 in 3 million, a mistake that was adopted by the judge in the summing up to the jury. A retrial was ordered (at which he was convicted again, but this time not based upon a mathematical error).