1.4 Measuring shapes

As well as measuring the brightnesses and sizes of astronomical objects, images allow us to measure and interpret their shapes and structures.

Stars are simple objects that are usually close to spherical. In most cases we cannot obtain information about their shapes and structure from images (deviations from a spherical shape can sometimes be identified by other means, e.g. variability). But the shapes and structure of a diverse range of other astronomical systems – for example, star-forming regions, galaxies and their sub-components, jets of material produced by stars and black holes – can be examined using images across the electromagnetic spectrum.

Remember that our images show the distribution of light as it is recorded by our telescope detector, which is located at a particular position in space. The detector records a two-dimensional image, but the light originates from a three-dimensional object.

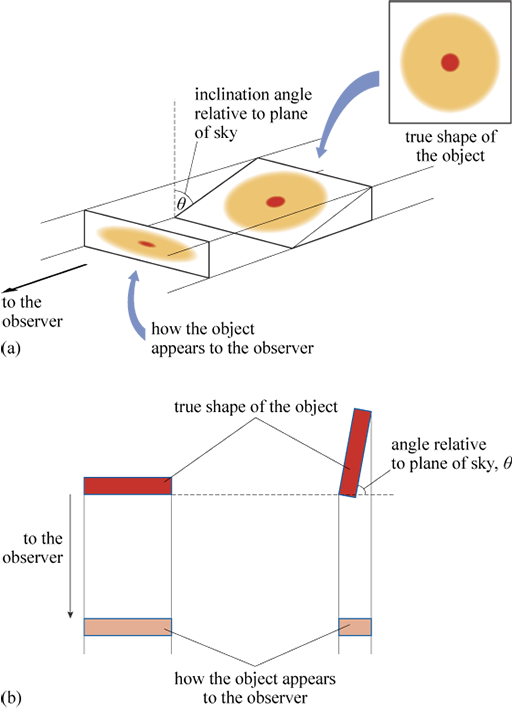
We are used to 2D images of 3D scenes from ordinary cameras. However, to interpret a photo of a landscape, or a group of people at a party, we have a wealth of extra information – from lighting, shadows, and our own intuition about the contents of the picture – to help our brains interpret the photo as a three-dimensional scene. Astronomical images often have fewer clues available to help us work out the underlying three-dimensional shapes, as shown in Figure 6.

Figure 6a shows an astronomical object shaped like a dinner plate (perhaps a galaxy) as viewed from three different directions. This scene depicts the effect of projection, where the object is tilting away from the plane of the sky. Note that this situation is mathematically similar to an inclined elliptical orbit.

Figure 6b shows the effect of orientation on the inferred length of a linear extended structure (perhaps an extended gas cloud or a jet-like feature).

Maximise

Figure 6 The effects of orientation on measured sizes and shapes of astronomical objects: (a) a disc-shaped object, and (b) a rod-shaped object.

Show description|Hide description

The effect of projection on astronomical objects is shown using two illustrations.

The top panel, Figure 6a, shows the projection of a disc-like structure, perhaps a galaxy or protostar. An inset in the top-right shows that the true shape of the object is circular.

The remainder of this panel shows how this circle is oriented compared to the plane of the sky. In the middle of the panel, a wedge is shown, onto which the circle has been placed. The wedge is inclined from the plane of the sky by an angle theta, such that if theta is zero the circle’s face is presented to the observer, while if theta is 90 degrees, the circle’s edge is presented to the observer.

At the left-hand edge of the figure, a third image is shown, representing how the projected circle appears to the observer. It is flattened along the axis of the wedge, so that it appears to the observer as an oval. The oval has been placed in a box, representing the observer’s camera, and diagonal lines connect the corners of this box back to the corners of the wedge, to indicate how the height of the wedge changes the flattening of the oval.

The bottom panel, Figure 6b, shows the projection of a rod-like structure, perhaps a filament in a gas cloud. Two different inclinations are shown. In the left-hand image, the rod is horizontal, indicating zero inclination to the plane of the sky. Lines are drawn straight down from the edges of this rod. At the bottom of these vertical lines, a second, identical rod is shown, with a description indicating that this is how the rod appears to the observer: i.e., the full length of the rod can be seen.

The right-hand image shows the rod being rotated by an inclination angle theta, so that it lies diagonally on the page. When lines are drawn straight down from this rod, towards the observer, the lines are much closer because of this rotation. A second, horizontal rod drawn between these lines is therefore much shorter. This is how the inclined rod appears to the observer, foreshortened because of the rod’s inclination.

Figure 6 The effects of orientation on measured sizes and shapes of astronomical objects: (a) a disc-shaped object, and (b) a rod-shaped ...

For a circular disc-like object, the observed major axis (i.e. twice the semimajor axis) corresponds to the true diameter of the disc, and the inclination angle (tilt, ) relative to the plane of the sky is given by

where is the measured semimajor axis and the measured semiminor axis.

If a linear object is projected at an angle of to the plane of the sky, then its true length, , is related to its measured length, , by

The conclusion to draw from these calculations is that frequently in astronomy we cannot be certain of the true shape or dimensions of objects. If you had not assumed the galaxy in the example was a circular disc, you could not have obtained the inclination angle.

Sometimes the problem can be solved by using additional information, such as that obtained from the spectrum of an object. The shift of spectral lines, or their broadened widths, may be caused by the Doppler effect which can provide clues about the motion or rotation of the object concerned. If we are studying very large samples, we sometimes expect that overall the orientations are random, which enables the use of statistical methods or computer simulations to determine the overall size and shape distributions of a set of objects. However, unknown orientation angles remain a major uncertainty in many astronomical studies.